Advertisements
Advertisements
Question
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

Solution
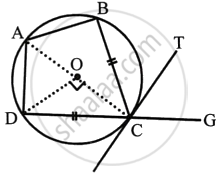
Join OC, OD and AC
i. ∠BCG + ∠BCD = 180° ...(Linear pair)
`=>` 108° + ∠BCD = 180° ...(∵ ∠BCG = 108° given)
`=>` ∠BCD = 180° – 108° = 72°
BC = CD ...(Given)
∴ ∠DCP = ∠BCT
But, ∠BCT + ∠BCD + ∠DCP = 180°
∴ ∠BCT + ∠BCT + 72° = 180° ...(∵ ∠DCP = ∠BCT)
2∠BCT = 180° – 72° = 108°
∴ ∠BCT = `108^circ/2` = 54°
ii. PCT is a tangent and CA is a chord.
∠CAD = ∠BCT = 54°
But arc DC subtends ∠DOC at the centre and ∠CAD at the remaining part of the circle.
∴ ∠DOC = 2∠CAD
= 2 × 54°
= 108°
APPEARS IN
RELATED QUESTIONS
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
In the following figure, O is the centre of the circle. Find the values of a, b and c.
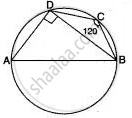
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

In the given figure, if ∠ ACE = 43° and ∠CAF = 62°. Find the value of a, b, and c.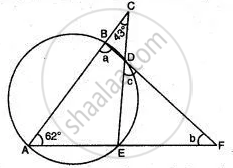
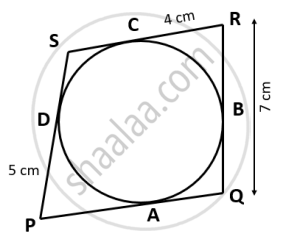
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: