Advertisements
Advertisements
Question
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
Solution
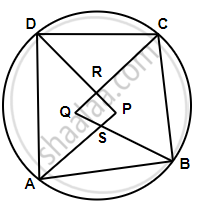
Given – ABCD is a cyclic quadrilateral and PQRS is a quadrilateral formed by the angle bisectors of angle ∠A, ∠B, ∠C and ∠D
To prove – PQRS is a cyclic quadrilateral.
Proof – In ΔAPD,
∠PAD + ∠ADP + ∠APD = 180° ...(1)
Similarly, In ∆BQC,
∠QBC + ∠BCQ + ∠BQC = 180° ...(2)
Adding (1) and (2), we get
∠PAD + ∠ADP + ∠APD + ∠QBC + ∠BCQ + ∠BQC = 180° + 180°
`=>` ∠PAD + ∠ADP + ∠QBC + ∠BCQ + ∠APD + ∠BQC = 360°
But ∠PAD + ∠ADP + ∠QBC + ∠BCQ
= `1/2` [∠A + ∠B + ∠C + ∠D]
= `1/2 xx 360^circ`
= 180°
∴ ∠APD + ∠BQC = 360° – 180° = 180° ...[From (3)]
But these are the sum of opposite angles of quadrilateral PRQS.
∴ Quad. PRQS is a cyclic quadrilateral.
APPEARS IN
RELATED QUESTIONS
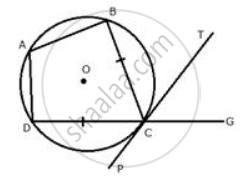
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
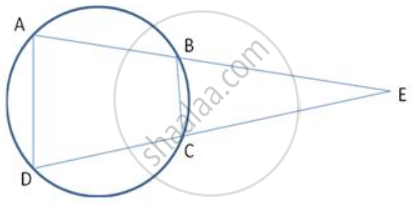
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
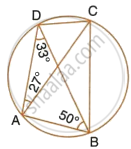
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.