Advertisements
Advertisements
Question
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

Solution
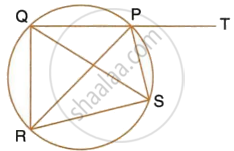
PQRS is a cyclic quadrilateral
∠QRS + ∠QPS = 180° ...(i)
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
Also, ∠QPS + ∠SPT = 180° ...(ii)
(Straight line QPT)
From (i) and (ii)
∠QRS = ∠SPT ...(iii)
Also, ∠RQS = ∠RPS ...(iv)
(Angle subtended by the same chord on the circle are equal)
And ∠RPS = ∠SPT
(PS bisects ∠RPT) ...(v)
From (iii), (iv) and (v)
∠QRS = ∠RQS
`=>` SQ = SR
APPEARS IN
RELATED QUESTIONS
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

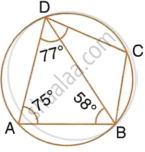
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
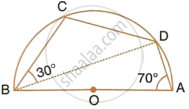
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
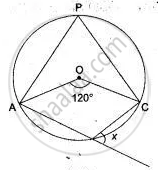
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

If O is the centre of the circle, find the value of x in each of the following figures