Advertisements
Advertisements
Question
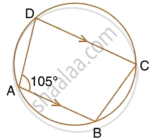
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

Solution

i. ∠BCD + ∠BAD = 180°
(Sum of opposite angles of a cyclic quadrilateral is 180°)
`=>` ∠BCD = 180° – 105° = 75°
ii. Now, AB || CD
∴ ∠BAD + ∠ADC = 180°
(Interior angles on the same side of parallel lines is 180°)
`=>` ∠ADC = 180° – 105° = 75°
iii. ∠ADC + ∠ABC = 180°
(Sum of opposite angles of a cyclic quadrilateral is 180°)
`=>` ∠ABC = 180° – 75° = 105°
APPEARS IN
RELATED QUESTIONS
In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
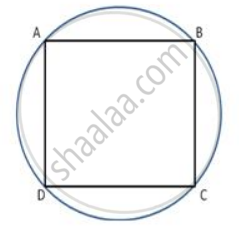
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
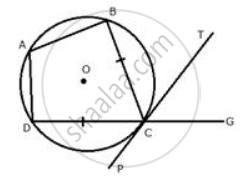
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
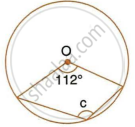
In the following figure, O is the centre of the circle. Find the values of a, b and c.
In the figure, given below, find: ∠ADC, Show steps of your working.
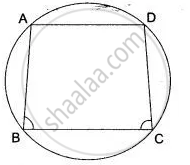
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.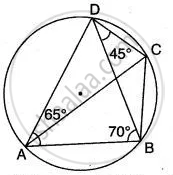
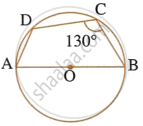
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA
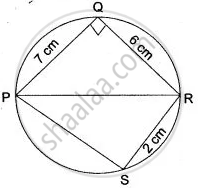
In the figure alongside PR is a diameter of the circle, PQ = 7 cm; QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.