Advertisements
Advertisements
Question
In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

Solution

i. ABCD is a cyclic quadrilateral
∴ ∠BAD + ∠BCD = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
`=>` ∠BCD = 180° – 96° = 84°
∴ ∠BCE = 180° – 84° = 96°
Similarly, BCEF is a cyclic quadrilateral
∴ ∠BCE + ∠BFE = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
∴ ∠BFE = 180° – 96° = 84°
ii. Now, ∠BAD + ∠BFE
= 96° + 84°
= 180°
But these two are interior angles on the same side of a pair of lines AD and FE
∴ AD || FE
APPEARS IN
RELATED QUESTIONS
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L. Show that:
- ∠ONL + ∠OML = 180°
- ∠BAM + ∠BMA
- ALOB is a cyclic quadrilateral.
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
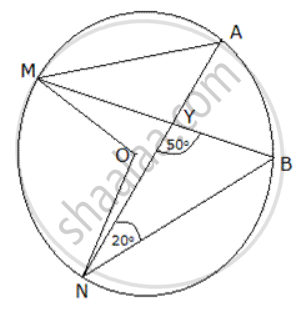
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
If O is the centre of the circle, find the value of x in each of the following figures