Advertisements
Advertisements
Question
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of Δ DEF are 90° - `"A"/2` , 90° - `"B"/2` and 90° - `"C"/2` respectively.
Solution
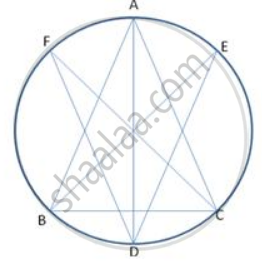
Since AD , BE and CF are bisectors of ∠ A , ∠ B and ∠ C respectively.
∴ ∠1 = ∠ 2 = ∠`"A"/2`
∠3 = ∠4 = ∠`"B"/2`
∠5= ∠6 = ∠`"C"/2`
∠ADE = ∠3 ....(1)
Also ∠ADF = ∠6 ....(2) (angles in the same segment)
Adding (1) and (2)
∠ADE + ∠ADF = ∠3 + ∠6
∠D = `1/2`∠B + `1/2` ∠C
∠D = `1/2` (B + ∠C) = `1/2` (180 - ∠A) (∠A + ∠B + ∠C = 180°)
∠D = 90 - `1/2` ∠A
Similarly ,
∠E = 90 - `1/2` ∠B , ∠F = 90 - `1/2` ∠C
APPEARS IN
RELATED QUESTIONS
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
In following fig., O is the centre of the circle. Find ∠ CBD.
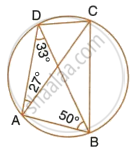
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.
Prove that the angle bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (Provided they are not parallel) intersect at the right angle.
In the figure , Δ PQR is an isosceles triangle with PQ = PR, and m ∠ PQR = 35°. Find m ∠ QSR and ∠ QTR.