Advertisements
Advertisements
Question
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.
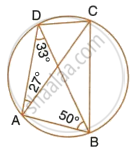
Solution
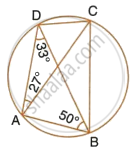
∠DAB + ∠DCB = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
`=>` 27° + ∠CAB + 83° = 180°
`=>` ∠CAB = 180° – 110° = 70°
APPEARS IN
RELATED QUESTIONS
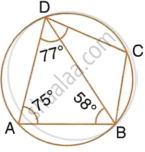
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

