Advertisements
Advertisements
Question
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
Solution
Let ABCD be a cyclic quadrilateral such that its diagonals AC and BD intersect in P at right angles.
Let PL ⊥ AB such that LP produced to meet CD in M. We have to prove that M bisects CD. i.e.,
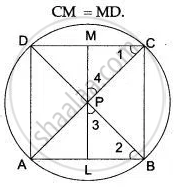
Consider arc AD, Clearly, it makes angles ∠ 1 and ∠2 in the same segment.
∠ 1 = ∠ 2 ...(i)
In the right-angled triangle PLB, we have
∠ 2 + ∠ 3 + ∠ PLB = 180°
⇒ ∠ 2 + ∠ 3 + 90° = 180°
⇒ ∠ 2 + ∠ 3 = 90° ....(ii)
Since, LPM is a straight line.
∴ ∠ 3 + ∠ BPD + ∠ 4 = 180°
⇒ ∠ 3 + 90° + ∠ 4 = 180°
⇒ ∠ 3 + ∠ 4 = 90° ...(iii)
From (ii) and (iii), we get
∠ 2 + ∠ 3 = ∠ 3 + ∠ 4
∠ 2 = ∠ 3 ...(iv)
From (i) and (iv), we get
∠ 1 = ∠ 4
PM = CM
Similarly,
PM = DM
Hence, CM = MD
Hence proved.
APPEARS IN
RELATED QUESTIONS
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130o. Find:
1) ∠DAB
2) ∠DBA

In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.
Calculate:
- ∠DBC,
- ∠DCB,
- ∠CAB.

In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
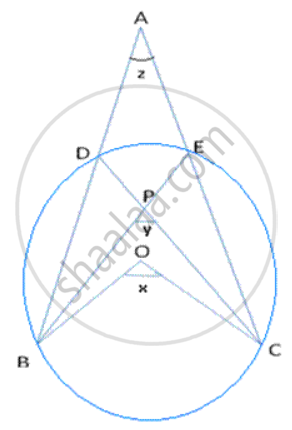
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
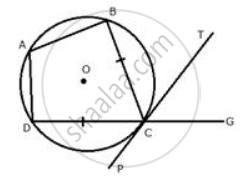
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
ABCD is a cyclic quadrilateral AB and DC are produced to meet in E. Prove that Δ EBC ∼ Δ EDA.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle, to prove the theorem complete the activity.
Given: ABCD is cyclic,
`square` is the exterior angle of ABCD
To prove: ∠DCE ≅ ∠BAD
Proof: `square` + ∠BCD = `square` .....[Angles in linear pair] (I)
ABCD is a cyclic.
`square` + ∠BAD = `square` ......[Theorem of cyclic quadrilateral] (II)
By (I) and (II)
∠DCE + ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
