Advertisements
Advertisements
Question
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
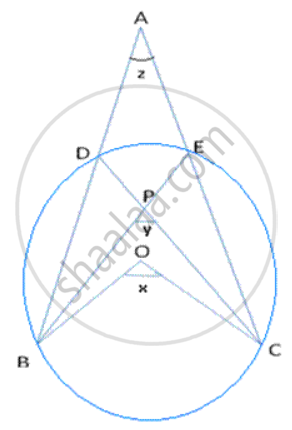
Solution
Since arc BC makes ∠ BOC at the centre and ∠ BDC on the remaining part of the circle
`therefore angle "BDC" = 1/2 angle "BOC" = 1/2 ("x") = 1/2 "x"`
∠BDC = ∠ BEC = ∠ `"x"/2` (angles in the same segment)
∠ ADB = AEP = 180 - ∠`"x"/2`
Also , ∠BPC = ∠DPE = ∠ Y (Vertically opposite)
In quadrilateral ADPE ,
∠ADP + ∠DEP + ∠PEA + ∠EAD = 360°
180 - ∠`"x"/2` + ∠ Y + 180 - ∠ `"x"/2` + z = 360°
- ∠ x + ∠ y + ∠ z = 0
∠ x = ∠ y+ ∠ z
APPEARS IN
RELATED QUESTIONS
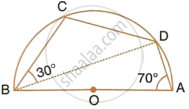
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
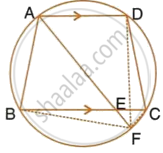
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
Prove that any four vertices of a regular pentagon are concylic (lie on the same circle).
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
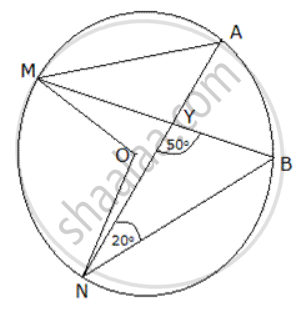
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
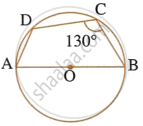
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
