Advertisements
Advertisements
प्रश्न
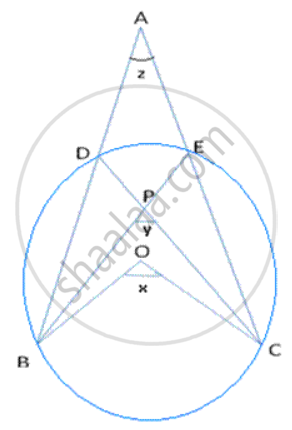
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
उत्तर
Since arc BC makes ∠ BOC at the centre and ∠ BDC on the remaining part of the circle
∠BDC = ∠ BEC = ∠
∠ ADB = AEP = 180 - ∠
Also , ∠BPC = ∠DPE = ∠ Y (Vertically opposite)
In quadrilateral ADPE ,
∠ADP + ∠DEP + ∠PEA + ∠EAD = 360°
180 - ∠
- ∠ x + ∠ y + ∠ z = 0
∠ x = ∠ y+ ∠ z
APPEARS IN
संबंधित प्रश्न
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

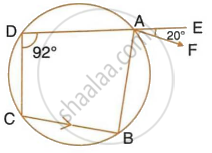
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65 ° , find the remaining angles
In a circle with centre O , chords AB and CD intersets inside the circle at E . Prove that ∠ AOC = ∠ BOD = 2 ∠ AEC.
In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

