Advertisements
Advertisements
Question
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
Solution
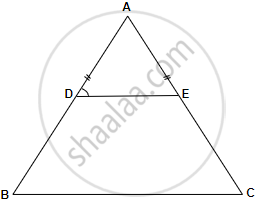
Given – In ∆ABC, AB = AC and D and E are points on AB and AC such that AD = AE. DE is joined.
To prove – B, C, E, D are concyclic.
Proof – In ∆ABC, AB = AC
∴ ∠B = ∠C ...[Angles opposite to equal sides]
Similarly, In ∆ADE, AD = AE ...[Given]
∴ ∠ADE = ∠AED ...[Angles opposite to equal sides]
In ∆ABC,
∴ `(AD)/(AB) = (AE )/(AC)`
∴ DE || BC
∴ ∠ADE = ∠B ...[Corresponding angles]
But ∠B = ∠C ...[Proved]
∴ Ext ∠ADE = Its interior opposite ∠C
∴ BCED is a cyclic quadrilateral
Hence B, C, E and D are concyclic.
APPEARS IN
RELATED QUESTIONS
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

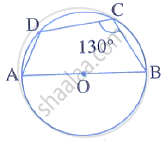
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
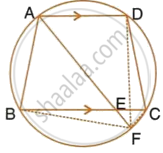
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
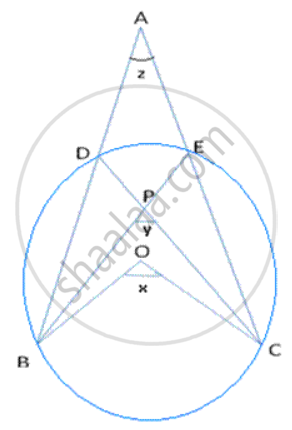
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

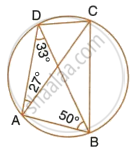
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

