Advertisements
Advertisements
Question
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
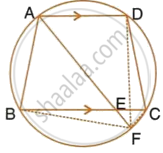
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
Solution
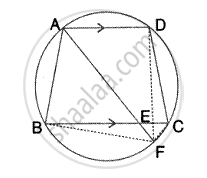
Given – ABCD is a cyclic quadrilateral in which AD || BC.
Bisector of ∠A meets BC at E and the given circle at F.
DF and BF are joined.
To prove –
- EF = FC
- BF = DF
Proof – ABCD is a cyclic quadrilateral and AD || BC
∵ AF is the bisector of ∠A, ∠BAF = ∠DAF
Also, ∠DAE = ∠BAE
∠DAE = ∠AEB ...[Alternate angles]
i. In ΔABE, ∠ABE = 180° – 2∠AEB
∠CEF = ∠AEB ...[Vertically opposite angles]
∠ADC = 180° – ∠ABC
= 180° – (180° – 2∠AEB)
∠ADC = 2∠AEB
∠AFC = 180° – ∠ADC
= 180° – 2∠AEB ...[Since ADFC is a cyclic quadrilateral]
∠ECF = 180° – (∠AFC + ∠CEF)
= 180° – (180° – 2∠AEB + ∠AEB)
= ∠AEB
∴ EF = FC
ii. ∴ Arc BF = Arc DF ...[Equal arcs subtends equal angles]
`=>` BF = DF ...[Equal arcs have equal chords]
Hence proved.
APPEARS IN
RELATED QUESTIONS
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
In the following figure, Prove that AD is parallel to FE.

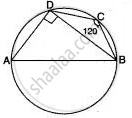
In the adjoining figure, AB is the diameter of the circle with centre O. If ∠BCD = 120°, calculate:
(i) ∠BAD (ii) ∠DBA
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.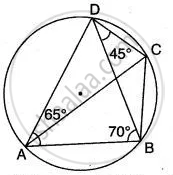
If O is the centre of the circle, find the value of x in each of the following figures
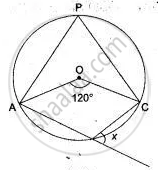
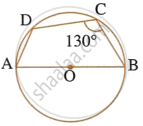
In the given figure, AB is the diameter of a circle with centre O.
∠BCD = 130°. Find:
- ∠DAB
- ∠DBA