Selina solutions for Mathematics [English] Class 10 ICSE chapter 17 - Circles [Latest edition]

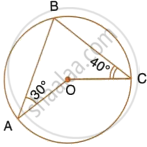
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. Find ∠AOC . Show your steps of working.

In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°

1. Prove that AC is a diameter of the circle.
2. Find ∠ACB.

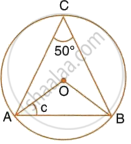
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:

1. ∠OCA,
2. ∠OAC.

In the following figure, O is the centre of the circle. Find the values of a, b and c.

In the following figure, O is the centre of the circle. Find the values of a, b and c.

In the following figure, O is the centre of the circle. Find the value of a, b, c and d.

In the following figure, O is the centre of the circle. Find the values of a, b, c and d.

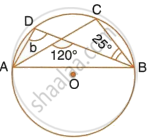
In the following figure, O is the centre of the circle. Find the values of a, b, c and d

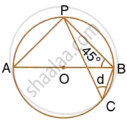
In the following figure, O is the centre of the circle. Find the values of a, b, c and d.

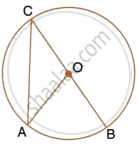
In the figure, AB is common chord of the two circles. If AC and AD are diameters; prove that D, B and C are in a straight line. O₁ and O₂ are the centers of two circles.

In the figure, given below, find:

1. ∠BCD,
2. ∠ADC,
3. ∠ABC.

Show steps of your working.

In the figure, given below, find: ∠ADC, Show steps of your working.

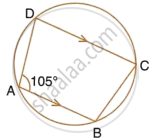
In the figure, given below, find: ∠ABC. Show steps of your working.

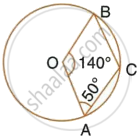
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:

1. ∠ACB, 
2. ∠OBC, 
3. ∠OAB, 
4. ∠CBA.

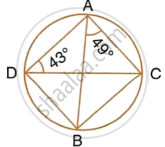
Calculate:

1. ∠CDB,
2. ∠ABC,
3. ∠ACB.

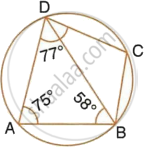
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:

1. ∠BDC,
2. ∠BCD,
3. ∠BCA.

In the following figure, O is centre of the circle and ΔABC is equilateral.

Find: 

1. ∠ADB,
2. ∠AEB.

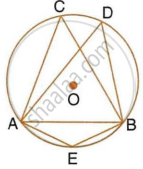
Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.

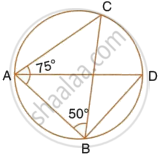
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

In the figure, given alongside, AOB is a diameter of the circle and ∠AOC = 110°. Find ∠BDC.

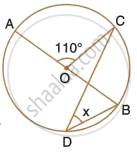
In the following figure, O is the centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.

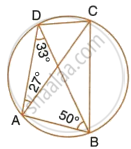
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°.

Calculate:

1. ∠DBC,
2. ∠DCB,
3. ∠CAB.

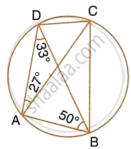
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.

In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠CAB.

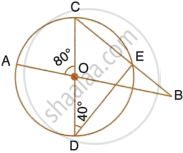
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in:

1. ∠DCE,
2. ∠ABC.

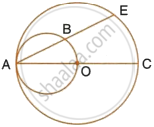
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in ∠ABC.

In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that : AB = BE.

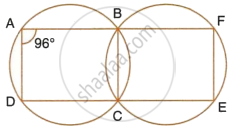
In the following figure,

1. if ∠BAD = 96°, find ∠BCD and ∠BFE.
2. Prove that AD is parallel to FE.

In the following figure, Prove that AD is parallel to FE.

ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.

Prove that the parallelogram, inscribed in a circle, is a rectangle.

Prove that the rhombus, inscribed in a circle, is a square.

In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.

Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.

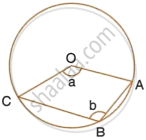
The figure given below, shows a circle with centre O. Given : ∠AOC = a and ∠ABC = b. 

1. Find the relationship between a and b.

2. Find the measure of angle OAB, if OABC is a parallelogram.

Two chords AB and CD intersect at P inside the circle. Prove that the sum of the angles subtended by the arcs AC and BD at the centre O is equal to twice the angle APC.

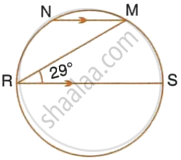
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠RNM

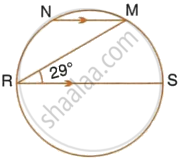
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM

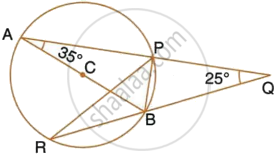
In the figure, given alongside, AB || CD and O is the centre of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

Two circles intersect at P and Q. Through P, a straight line APB is drawn to meet the circles in A and B. Through Q, a straight line is drawn to meet the circles at C and D. Prove that AC is parallel to BD.

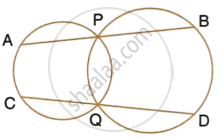
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.

AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PRB

AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PBR

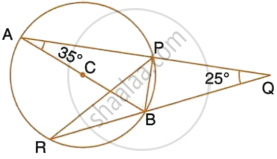
AB is a diameter of the circle APBR, as shown in the figure. APQ and RBQ are straight lines. Find : ∠BPR

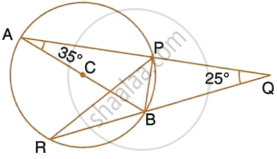
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

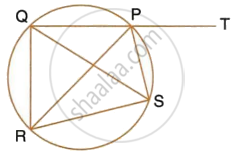
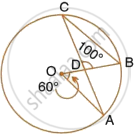
In the figure, O is the centre of the circle, ∠AOE = 150°, ∠DAO = 51°. Calculate the sizes of the angles CEB and OCE.

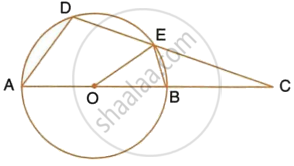
In the figure, given below, P and Q are the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x .

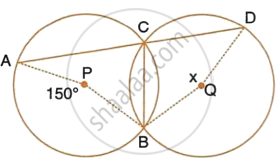
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.

Calculate, in terms of a°, the value of : obtuse ∠AOB,

Give reasons for your answers clearly.

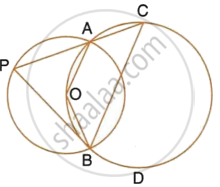
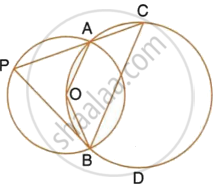
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.

Calculate, in terms of a°, the value of : ∠ACB,

Give reasons for your answers clearly.

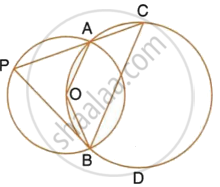
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.

Calculate, in terms of a°, the value of : ∠ADB.

Give reasons for your answers clearly.

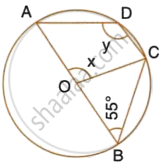
In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.

In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that : ∠BCD = 2∠ABE.

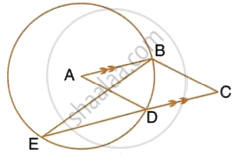
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :

1. ∠DAB,
2. ∠BDC.

In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°.

Calculate:

1. ∠EBA,
2. ∠BCD.

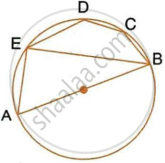
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD. 

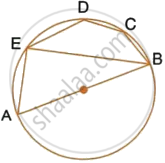
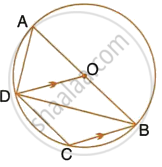
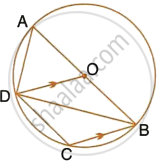
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°. 

Calculate : ∠DBA 

Also, show that the ΔAOD is an equilateral triangle.

In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°. 

Calculate : ∠DBC 

Also, show that the ΔAOD is an equilateral triangle.

In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°. 

Calculate : ∠ADC 

Also, show that the ΔAOD is an equilateral triangle.

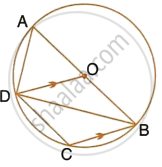
In the given figure, I is the incentre of ΔABC. BI when produced meets the circumcircle of ΔABC at D. ∠BAC = 55° and ∠ACB = 65°; calculate:

1. ∠DCA,
2. ∠DAC,
3. ∠DCI,
4. ∠AIC.

A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that:

1. ∠ABC = 2∠APQ,
2. ∠ACB = 2∠APR,
3. `∠QPR = 90^circ - 1/2 ∠BAC`.

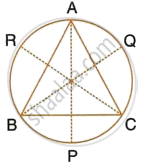
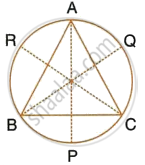
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that : 

∠ACB = 2∠APR,

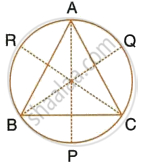
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that : 

`∠QPR = 90^circ - 1/2 ∠BAC`

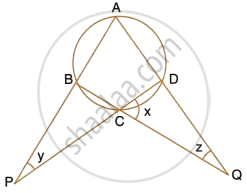
Calculate the angles x, y and z if :

`x/3 = y/4 = z/5`

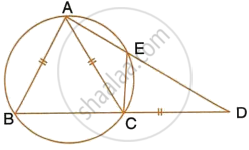
In the given figure, AB = AC = CD and ∠ADC = 38°. Calculate :

1. Angle ABC
2. Angle BEC

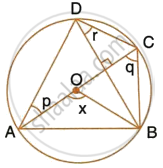
In the given figure, AC is a diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, q and r in terms of x.

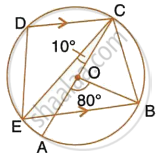
In the given figure, AC is the diameter of the circle with centre O. CD and BE are parallel. Angle ∠AOB = 80° and ∠ACE = 10°.

Calculate:

1. Angle BEC,
2. Angle BCD,
3. Angle CED.

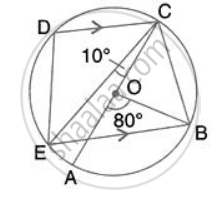
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80^o and angle ACE = 10^o. Calculate : Angle BCD

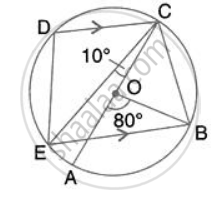
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80^o and angle ACE = 10^o. Calculate: Angle CED.

In the given figure, AE is the diameter of the circle. Write down the numerical value of ∠ABC + ∠CDE. Give reasons for your answer.

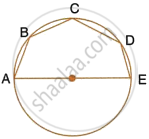
In the given figure, AOC is a diameter and AC is parallel to ED. If ∠CBE = 64°, calculate ∠DEC.

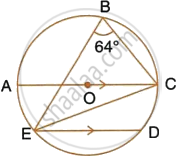
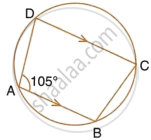
Use the given figure to find:

1. ∠BAD,
2. ∠DQB.

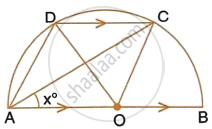
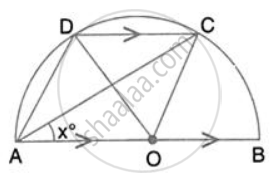
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠CAB = x°; find (in terms of x) the values of :

1. ∠COB,
2. ∠DOC,
3. ∠DAC,
4. ∠ADC.

In the given figure, AOB is a diameter and DC is parallel to AB. If  ∠ CAB = x^o ; find (in terms of x) the values of: ∠ DOC.

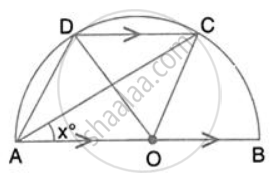
In the given figure, AOB is a diameter and DC is parallel to AB. If  ∠ CAB = x^o ; find (in terms of x) the values of: ∠ DAC

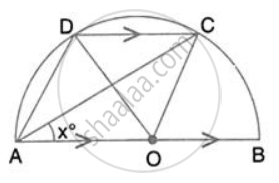
In the given figure, AOB is a diameter and DC is parallel to AB. If  ∠ CAB = x^o ; find (in terms of x) the values of: ∠ ADC.

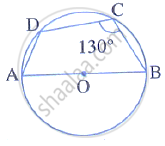
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA

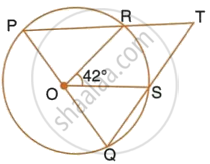
In the given figure, PQ is the diameter of the circle whose centre is O. Given ∠ROS = 42°, calculate ∠RTS.

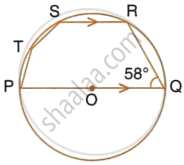
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°,

Calculate:

1. ∠RPQ,
2. ∠STP.

AB is the diameter of the circle with centre O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of : 

1. ∠ABD,
2. ∠DBC, 
3. ∠ADC. 

AB is the diameter of the circle with centre O. OD is parallel to BC and  ∠ AOD = 60° ; calculate the numerical values of:  ∠ DBC 

AB is the diameter of the circle with centre O. OD is parallel to BC and  ∠ AOD = 60° ; calculate the numerical values of:  ∠ ADC

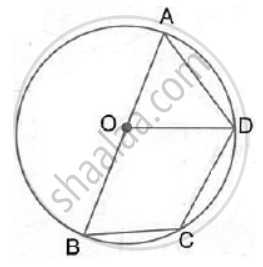
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :

1. ∠AOB,
2. ∠ACB,
3. ∠ABD,
4. ∠ADB.

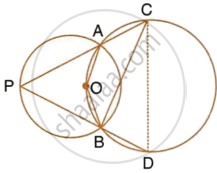
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :  ∠ACB 

In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :  ∠ABD 

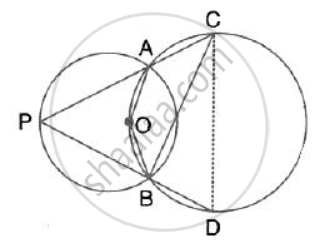
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :  ∠ADB  

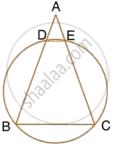
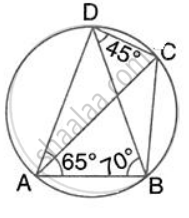
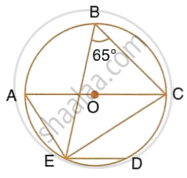
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find:

1. ∠BCD 
2. ∠ACB

Hence, show that AC is a diameter.

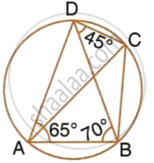
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find: ∠ ACB. 

Hence, show that AC is a diameter.

In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.

The given figure shows a circle with centre O and ∠ABP = 42°.

Calculate the measure of:

1. ∠PQB
2. ∠QPB + ∠PBQ

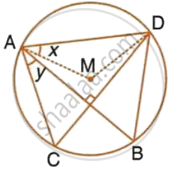
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. If ∠MAD = x and ∠BAC = y :

1. express ∠AMD in terms of x.
2. express ∠ABD in terms of y.
3. prove that : x = y.

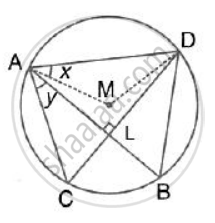
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other.

If ∠MAD = x and ∠BAC = y :  express ∠ABD in terms of y.

In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. 

If ∠MAD = x and ∠BAC = y , Prove that : x = y

In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.

In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate: ∠AEF

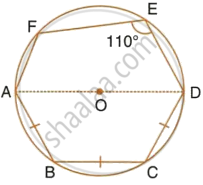
In the following figure, AD is the diameter of the circle with centre O. chords AB, BC and CD are equal. If ∠DEF = 110°, Calculate: ∠FAB.

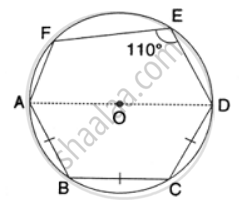
If two sides of a cyclic quadrilateral are parallel; prove that:

1. its other two sides are equal.
2. its diagonals are equal.

The given figure shows a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.

Calculate:

1. ∠POS, 
2. ∠QOR, 
3. ∠PQR.

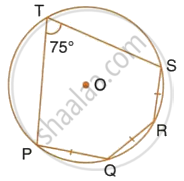
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:

1. ∠AOB, 
2. ∠ACB,
3. ∠ABC.

In a regular pentagon ABCDE, inscribed in a circle; find ratio between angle EDA and angle ADC.

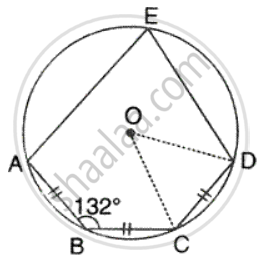
In the given figure, AB = BC = CD and ∠ABC = 132°.

Calcualte:

1. ∠AEB,
2. ∠AED,
3. ∠COD.

In the given figure, AB = BC = CD and ∠ABC = 132° . Calcualte: ∠AED

In the given figure, AB = BC = CD and ∠ABC = 132° . Calcualte: ∠ COD.

In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠CAB

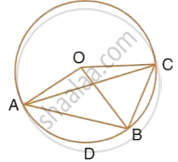
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠ADB.

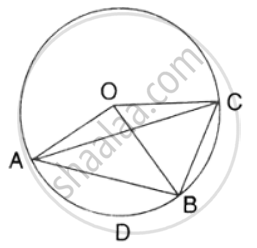
The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon. Find the angles of triangle ABC.

In the given figure, BD is a side of a regular hexagon, DC is a side of a regular pentagon and AD is a diameter.

Calculate :

1. ∠ADC,
2. ∠BDA,
3. ∠ABC,
4. ∠AEC.

In the given circle with diameter AB, find the value of x.

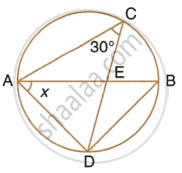
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.

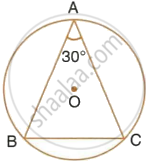
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.

In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.

The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.

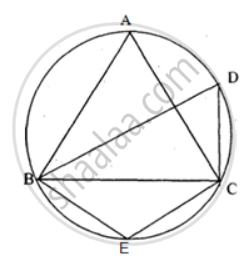
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BDC

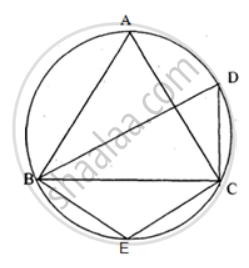
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BEC 

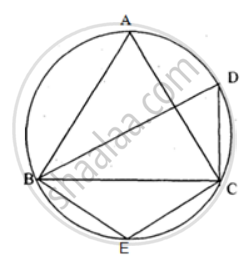
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC

D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.

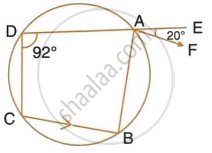
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.

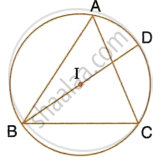
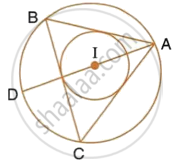
If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If ∠BAC = 66° and ∠ABC = 80°.

Calculate:

1. ∠DBC,
2. ∠IBC,
3. ∠BIC.

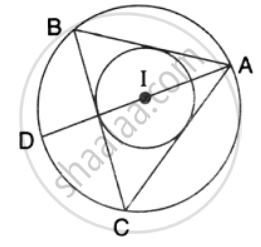
If I is the incentre of triangle ABC and AI when produced meets the cicrumcircle of triangle ABC in points D . if ∠BAC = 66° and ∠ABC = 80°. Calculate : ∠IBC

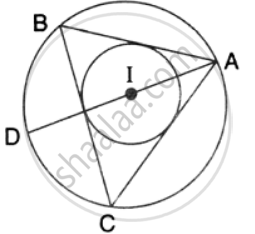
If I is the incentre of triangle ABC and AI when produced meets the cicrumcircle of triangle ABC in points D. f ∠BAC = 66° and ∠ABC = 80°. Calculate : ∠BIC.

In the given figure, AB = AD = DC = PB and ∠DBC = x°. Determine, in terms of x :

1. ∠ABD,
2. ∠APB.

Hence or otherwise, prove that AP is parallel to DB.

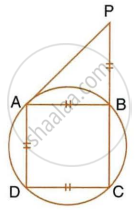
In the given figure; ABC, AEQ and CEP are straight lines. Show that ∠APE and ∠CQE are supplementary.

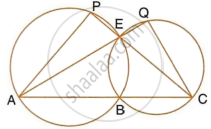
In the given figure, AB is the diameter of the circle with centre O.

If ∠ADC = 32°, find angle BOC.

In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.

In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.

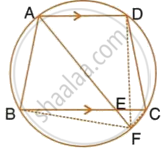
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:

1. EF = FC
2. BF = DF

ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F.  If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.

The following figure shows a circle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, find the perimeter of the cyclic quadrilateral PQRS.

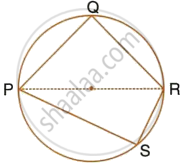
In the given figure, AB is the diameter of a circle with centre O.

If chord AC = chord AD, prove that:

1. arc BC = arc DB
2. AB is bisector of ∠CAD.

Further, if the length of arc AC is twice the length of arc BC, find:

1. ∠BAC
2. ∠ABC

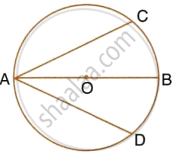
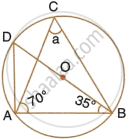
In cyclic quadrilateral ABCD; AD = BC, ∠BAC = 30° and ∠CBD = 70°; find:

1. ∠BCD
2. ∠BCA
3. ∠ABC
4. ∠ADC

In the given figure, ∠ACE = 43° and ∠CAF = 62°; find the values of a, b and c.

In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

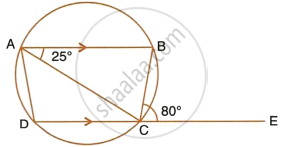
Find:

1. ∠CAD
2. ∠CBD
3. ∠ADC

ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB = 60°.

In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.

In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°.

Find: 

1. ∠BCD
2. ∠BCA
3. ∠ABC
4. ∠ADB

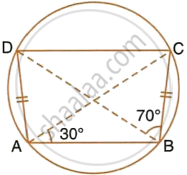
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find:

1. ∠OBD
2. ∠AOB
3. ∠BED

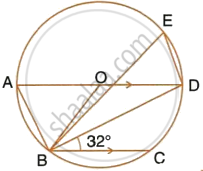
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. 

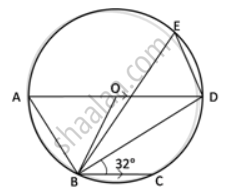
Find: ∠AOB

In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. 

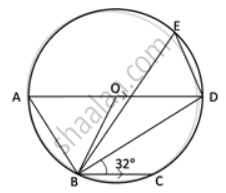
Find: ∠BED  

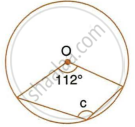
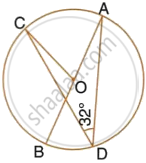
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:

1. ∠BCD
2. ∠BOD
3. ∠OBD