Advertisements
Advertisements
Question
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠CAB
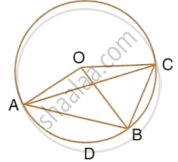
Solution
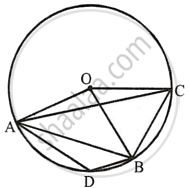
Join AD and DB
Arc B = 2 arc BC and ∠AOB = 180°
∴ ∠BOC = `1/2` ∠AOB
= `1/2 xx 108^circ`
= 54°
Now, Arc BC subtends ∠BOC at the centre and ∠CAB at the remaining part of the circle.
∴ ∠CAB = `1/2` ∠BOC
= `1/2 xx 54^circ`
= 27°
APPEARS IN
RELATED QUESTIONS
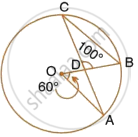
In the following figure, O is the centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.
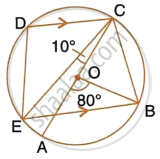
In the given figure, AC is the diameter of the circle with centre O. CD and BE are parallel. Angle ∠AOB = 80° and ∠ACE = 10°.
Calculate:
- Angle BEC,
- Angle BCD,
- Angle CED.
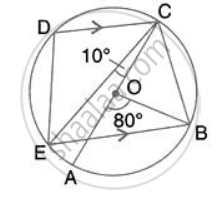
In the given figure, AB = BC = CD and ∠ABC = 132°.
Calcualte:
- ∠AEB,
- ∠AED,
- ∠COD.

The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon. Find the angles of triangle ABC.

In the given figure, BD is a side of a regular hexagon, DC is a side of a regular pentagon and AD is a diameter.
Calculate :
- ∠ADC,
- ∠BDA,
- ∠ABC,
- ∠AEC.

In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate: Angle CED.
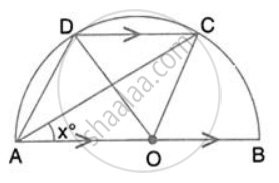
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ DOC.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ DBC
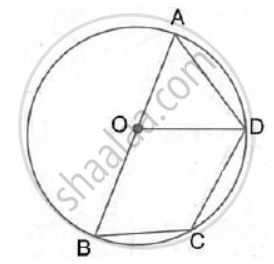
If O is the circumcentre of a Δ ABC and OD ⊥ BC, prove that ∠ BOD = ∠A.
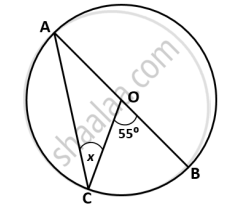
In the given figure, AB is a diameter of the circle with centre ‘O’. If ∠COB = 55⁰ then the value of x is: