Advertisements
Advertisements
Question
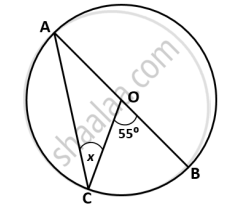
In the given figure, AB is a diameter of the circle with centre ‘O’. If ∠COB = 55⁰ then the value of x is:
Options
27.5°
55°
110°
125°
Solution
27.5°
Explanation:
∠CAB = `1/2` × ∠COB
The angle subtends at the circumference is half the angle subtend at the centre.
∠CAB = `1/2` × 55⁰
∠CAB = 27.5⁰
AO and CO are the radius of the same circle.
AO = CO
∴ ∠ACO = ∠CAO
∴ ∠CAB = ∠CAO = 27.5⁰
∴ x = ∠CAO = 27.5⁰
APPEARS IN
RELATED QUESTIONS
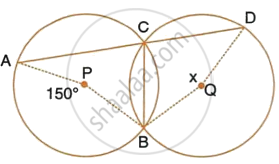
In the figure, given below, P and Q are the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x .
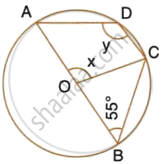
In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.
In the given figure, AE is the diameter of the circle. Write down the numerical value of ∠ABC + ∠CDE. Give reasons for your answer.
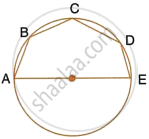
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠CAB = x°; find (in terms of x) the values of :
- ∠COB,
- ∠DOC,
- ∠DAC,
- ∠ADC.
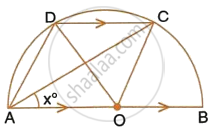
In the given figure, PQ is the diameter of the circle whose centre is O. Given ∠ROS = 42°, calculate ∠RTS.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ DBC
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ ADC
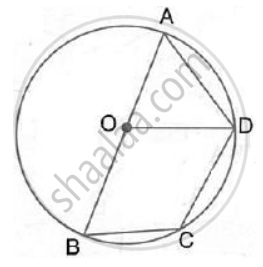
In a circle with center O, chords AB and CD intersect inside the circumference at E. Prove that ∠ AOC + ∠ BOD = 2∠ AEC.
If O is the circumcentre of a Δ ABC and OD ⊥ BC, prove that ∠ BOD = ∠A.
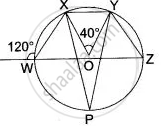
In the figure alongside O is the centre of circle ∠ XOY = 40°, ∠ TWX = 40° and XY is parallel to TZ.
Find: (i) ∠ XZY, (ii) ∠ YXZ (iii) ∠ TZY.