Advertisements
Advertisements
Question
In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.
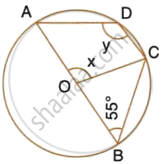
Solution

∠AOC = 2∠ABC = 2 × 55°
(Angle at the centre is double the angle at the circumference subtended by the same chord)
∴ x = 110°
ABCD is cyclic quadrilateral
∴ ∠ADC + ∠ABC = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary
`=>` y = 180° – 55° = 125°
APPEARS IN
RELATED QUESTIONS
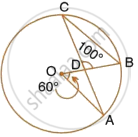
In the following figure, O is the centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.
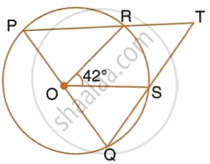
In the given figure, PQ is the diameter of the circle whose centre is O. Given ∠ROS = 42°, calculate ∠RTS.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of :
- ∠ABD,
- ∠DBC,
- ∠ADC.
In the given figure, AB = BC = CD and ∠ABC = 132°.
Calcualte:
- ∠AEB,
- ∠AED,
- ∠COD.

The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon. Find the angles of triangle ABC.

In the given figure, BD is a side of a regular hexagon, DC is a side of a regular pentagon and AD is a diameter.
Calculate :
- ∠ADC,
- ∠BDA,
- ∠ABC,
- ∠AEC.

The figure given below, shows a circle with centre O. Given : ∠AOC = a and ∠ABC = b.
-
Find the relationship between a and b.
-
Find the measure of angle OAB, if OABC is a parallelogram.
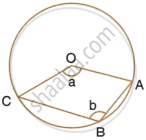
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate: Angle CED.
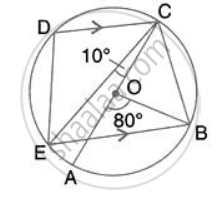
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ ADC.
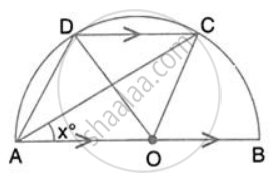
If O is the circumcentre of a Δ ABC and OD ⊥ BC, prove that ∠ BOD = ∠A.
