Advertisements
Advertisements
Question
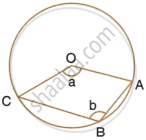
The figure given below, shows a circle with centre O. Given : ∠AOC = a and ∠ABC = b.
-
Find the relationship between a and b.
-
Find the measure of angle OAB, if OABC is a parallelogram.
Solution
i. ∠ABC = `1/2` Reflex (∠COA)
(Angle at the centre is double the angle at the circumference subtended by the same chord)
`=> b = 1/2 (360 - a)`
`=>` a + 2b = 360°
ii. Since OABC is a parallelogram, so opposite angles are equal.
2b + b = 360°
3b = 360°
b = 120°
∴ 120° + 120° + x + x = 360°
2x = 360° – 240°
2x = 120°
`x = (120^circ)/2`
x = 60°
`=>` ∠OAB = 60°
APPEARS IN
RELATED QUESTIONS
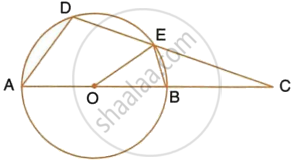
In the figure, O is the centre of the circle, ∠AOE = 150°, ∠DAO = 51°. Calculate the sizes of the angles CEB and OCE.
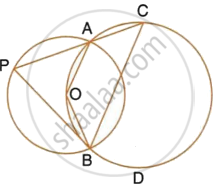
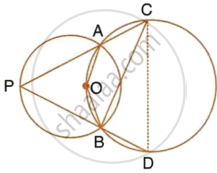
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : obtuse ∠AOB,
Give reasons for your answers clearly.
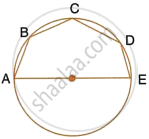
In the given figure, AE is the diameter of the circle. Write down the numerical value of ∠ABC + ∠CDE. Give reasons for your answer.
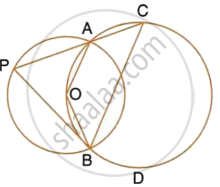
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :
- ∠AOB,
- ∠ACB,
- ∠ABD,
- ∠ADB.
In a regular pentagon ABCDE, inscribed in a circle; find ratio between angle EDA and angle ADC.
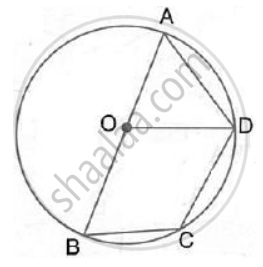
In the given figure, AB = BC = CD and ∠ABC = 132°.
Calcualte:
- ∠AEB,
- ∠AED,
- ∠COD.

The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : ∠ACB,
Give reasons for your answers clearly.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ ADC
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ADB

In a circle with center O, chords AB and CD intersect inside the circumference at E. Prove that ∠ AOC + ∠ BOD = 2∠ AEC.
