Advertisements
Advertisements
Question
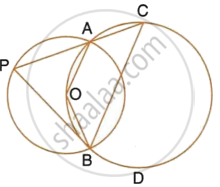
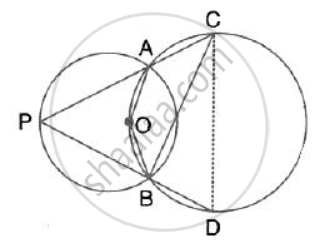
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : obtuse ∠AOB,
Give reasons for your answers clearly.
Solution
Obtuse ∠AOB = 2∠APB = 2a°
(Angle at the centre is double the angle at the circumference subtended by the same chord)
APPEARS IN
RELATED QUESTIONS
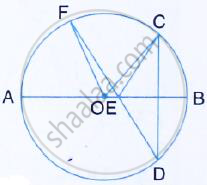
In the figure given below, AB is diameter of the circle whose centre is O. given that: ∠ECD =
∠EDC = 32°. Show that ∠COF = ∠CEF.
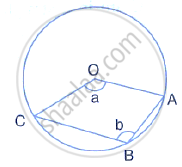
The figure given below, shows a Circle with centre O.
Given: ∠AOC = a and ∠ABC = b.
Find the relationship between a and b
In the given diagram, chord AB = chord BC.
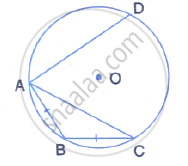
(i) what is the relation between arcs AB and BC?
(ii) what is the relation between ∠AOB and ∠BOC?
(iii) If arc AD is greater than arc ABC, then what is the relation between chords AD and AC?
(iv) If ∠AOB = 50°, find the measure of angle BAC.
In a regular pentagon ABCDE, inscribed in a circle; find ratio between angle EDA and angle ADC.
In the given figure, BD is a side of a regular hexagon, DC is a side of a regular pentagon and AD is a diameter.
Calculate :
- ∠ADC,
- ∠BDA,
- ∠ABC,
- ∠AEC.

In the given figure, AB is the diameter of the circle with centre O.
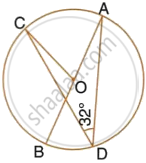
If ∠ADC = 32°, find angle BOC.
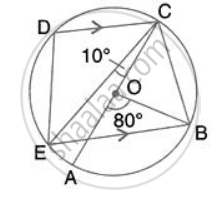
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate : Angle BCD
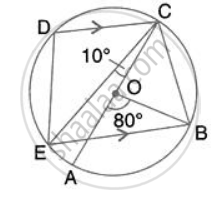
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate: Angle CED.
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ABD
Prove that the line segment joining the midpoints of two equal chords of a circle subtends equal angles with the chord.
