Advertisements
Advertisements
Question
Prove that the line segment joining the midpoints of two equal chords of a circle subtends equal angles with the chord.
Solution
Here, M and N are the mid-points of two equal chords AB and CD respectively of a circle with center O.
We have to prove that
∠BMN = ∠CNM
∠AMN = ∠DNM
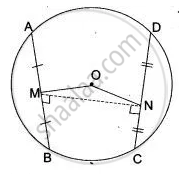
Join ON, OM and NM
∴ ∠OMA = ∠OMB = 90°
∠ OND = ∠ONC = 90° ....(i)(Line joining the centre and midpoint of a chord is perpendicular to the chord)
Since, AB = CD ⇒ OM = ON
∴ In ΔOMN, ∠OMN = ∠ONM ...(ii)
(i) ∠OMB = ∠ONC ...[ Using (i) and (ii) ]
∠OMN = ∠ONM
⇒ ∠OMB - ∠OMN = ∠ONC - ∠ONM
⇒ ∠BMN = ∠CNM
(ii) ∠OMA = ∠OND
∠OMN = ∠ONM ...[ Using (i) and (ii) ]
⇒ ∠OMA + ∠OMN = ∠OND + ∠ONM
⇒ ∠AMN = ∠DNM
Hence proved.
APPEARS IN
RELATED QUESTIONS
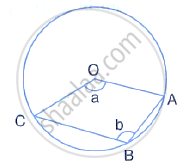
The figure given below, shows a Circle with centre O.
Given: ∠AOC = a and ∠ABC = b.
Find the relationship between a and b
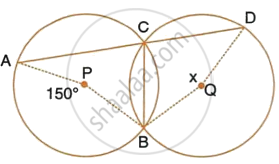
In the figure, given below, P and Q are the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x .
In the given figure, AB = BC = CD and ∠ABC = 132°.
Calcualte:
- ∠AEB,
- ∠AED,
- ∠COD.

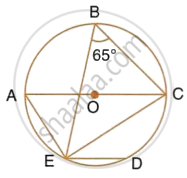
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
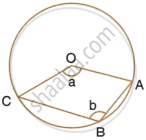
The figure given below, shows a circle with centre O. Given : ∠AOC = a and ∠ABC = b.
-
Find the relationship between a and b.
-
Find the measure of angle OAB, if OABC is a parallelogram.
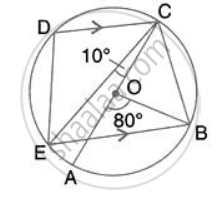
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate : Angle BCD
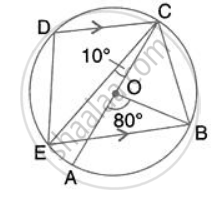
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate: Angle CED.
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ DOC.
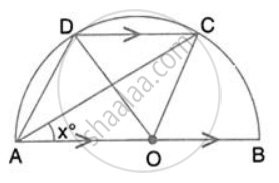
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ ADC
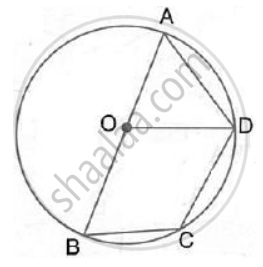
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ABD