Advertisements
Advertisements
Question
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
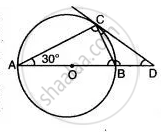
Solution
Join OC.
∠ ACB = 90° ...(Angle of the semicircle)
∠ ABC = 60° ...(Angle Sum property)
∠ CBD = 120° ...(adj to angle CBA 30°)
∠ OCD = 90° ...(tangent)
∠ COB = 60° ...(Angle at the center is equal to twice that of the circumference)
∠ OCB = 60° ...(Angle Sum property)
∠BCD = ∠ OCD - ∠OCB = 90° - 60° = 30°
∠BDC = ∠BCD = 30°
BD = BC
Hence proved.
APPEARS IN
RELATED QUESTIONS
A line intersecting a circle in two points is called a ______.
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

How many common tangents can be drawn to two circles, touching each
other externally?
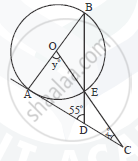
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
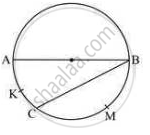
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

Tangents from an external point to a circle are ______
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
