Advertisements
Advertisements
Question
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Solution
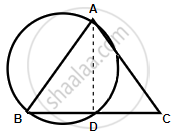
Join AD.
AB is the diameter.
∴ ∠ADB = 90° ...(Angle in a semi-circle)
But, ∠ADB + ∠ADC = 180° ...(Linear pair)
`=>` ∠ADC = 90°
In ΔABD and ΔACD,
∠ADB = ∠ADC ...(Each 90°)
AB = AC ...(Given)
AD = AD ...(Common)
ΔABD ≅ ΔACD ...(RHS congruence criterion)
`=>` BD = DC ...(C.P.C.T)
Hence, the circle bisects base BC at D.
APPEARS IN
RELATED QUESTIONS
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
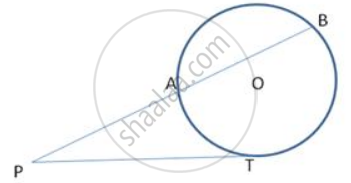
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
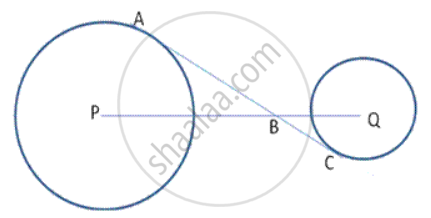
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
Two parallel lines touch the circle at
points A and B respectively. If the area of the circle is 25 n cm2, then AB is equal to ______
Find the value of ∠DCE.

In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
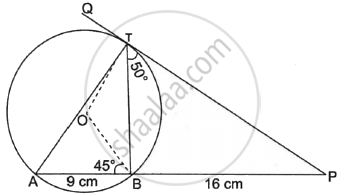
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT