Advertisements
Advertisements
Question
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
Solution
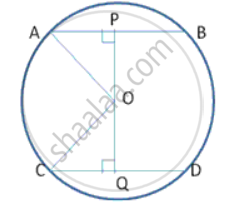
AP = PB = 3cm
CQ = QD = 6cm (Perpendicular from centre to a chord bisects the chord)
OA = OC = r (say)
Let OP = x, ∴ OQ = 3 - x
In right Δ OQC,
By Pythagoras theorem,
OC2 = OQ2 + CQ2
r2 = (3-x)2 + 62 ----(1)
Similarly, In Δ OPA,
OA2 = AP2 + PO2
r2 = 32 + x2 ----(2}
From (1) and {2}
(3-x)2 + 62 = 32+ x2
-6x + 36 = 0
x = 6
from {2}
r2 = 32 + 62 = 9 + 36 = 45
r = `3 sqrt 5`
Thus , radius of the circle is `3 sqrt 5` cm
APPEARS IN
RELATED QUESTIONS
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
In the given figure, find TP if AT = 16 cm and AB = 12 cm.

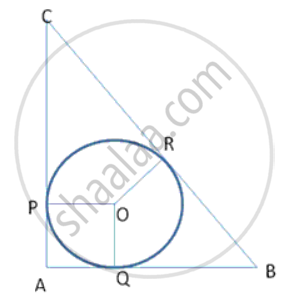
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
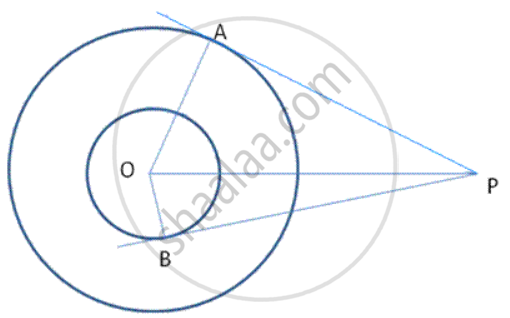
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.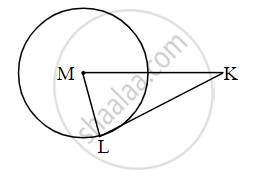
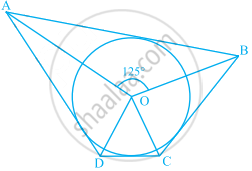
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

Find the value of ∠DCE.

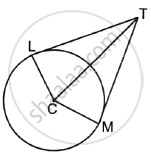
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.