Advertisements
Advertisements
प्रश्न
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
उत्तर
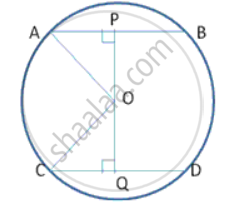
AP = PB = 3cm
CQ = QD = 6cm (Perpendicular from centre to a chord bisects the chord)
OA = OC = r (say)
Let OP = x, ∴ OQ = 3 - x
In right Δ OQC,
By Pythagoras theorem,
OC2 = OQ2 + CQ2
r2 = (3-x)2 + 62 ----(1)
Similarly, In Δ OPA,
OA2 = AP2 + PO2
r2 = 32 + x2 ----(2}
From (1) and {2}
(3-x)2 + 62 = 32+ x2
-6x + 36 = 0
x = 6
from {2}
r2 = 32 + 62 = 9 + 36 = 45
r = `3 sqrt 5`
Thus , radius of the circle is `3 sqrt 5` cm
APPEARS IN
संबंधित प्रश्न
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
The tangents drawn at the extremities of the diameter of a circle are ______.
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

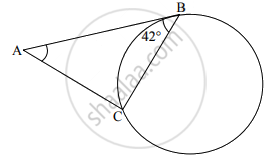
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
