Advertisements
Advertisements
प्रश्न
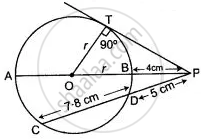
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
उत्तर
Given that,
CD = 7.8 cm, PD = 5 cm, PB = 4 cm
As we know,
PT2 = PD × PC
PT2 = PD × (PD + CD)
PT2 = 5 × 12.8
PT2 = 64
`=>` PT = 8 cm
Now in ΔPOT,
PO2 = OT2 + PT2
(r + 4)2 = r2 + 64
r2 + 16 + 8r = r2 + 64
8r = 48
r = 6
- Thus AB = 2r = 12 cm
- Length of tangent PT = 8 cm.
APPEARS IN
संबंधित प्रश्न
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.


In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = Scm, find PT.
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
