Advertisements
Advertisements
प्रश्न
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

उत्तर
Let ABC be the right angled triangle such that ∠B = 90° , BC = 6 cm, AB = 8 cm. Let O be the centre and r be the radius of the incircle.
AB, BC and CA are tangents to the circle at P, N and M.
∴ OP = ON = OM = r (radius of the circle)
By Pythagoras theorem,
CA2 = AB2 + BC2
⇒ CA2 = 82 + 62
⇒ CA2 = 100
⇒ CA = 10 cm
Area of ∆ABC = Area ∆OAB + Area ∆OBC + Area ∆OCA
APPEARS IN
संबंधित प्रश्न
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
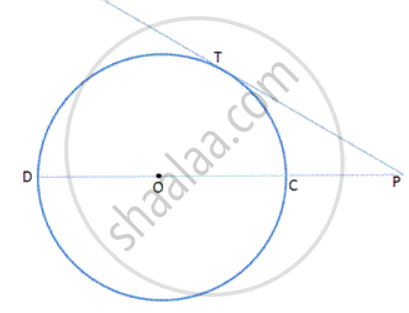
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
Find the value of ∠DCE.

In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
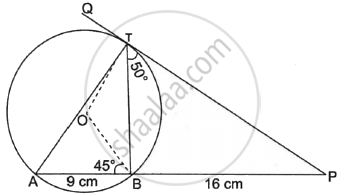
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT