Advertisements
Advertisements
प्रश्न
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
उत्तर

Steps of construction:
- Draw a circle with a radius of 5 cm with the centre as O.
- Take point A on the circumference of the circle and join OA.
- Draw a radius OB, making an angle of 120° (180° – 60°) with OA.
- Draw a perpendicular to OB at point B and a perpendicular to OA at point A. Let both perpendiculars intersect at point P.
- PA and PB are the required tangents at an angle of 60°.
APPEARS IN
संबंधित प्रश्न
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

Two parallel lines touch the circle at
points A and B respectively. If the area of the circle is 25 n cm2, then AB is equal to ______
Find the value of ∠DCE.

Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
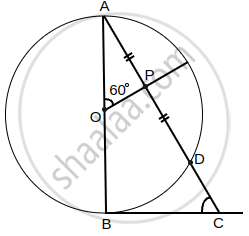
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
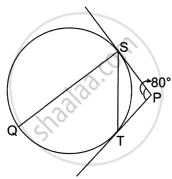
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.
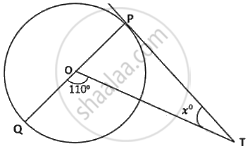
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.