Advertisements
Advertisements
प्रश्न
The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
उत्तर
Given the distance between two tangents parallel to each other to a circle is 13 cm.
Two parallel tangents to a circle are found when the line joining the point of contact are diameter.
∴ d = 13 cm
Since, r = `d/2 = 13/2` = 6.5 cm
Hence, radius of circle is 6.5 cm.
APPEARS IN
संबंधित प्रश्न
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
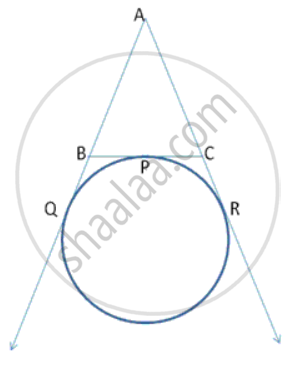
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
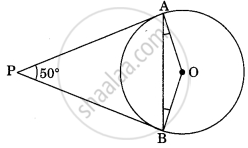
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
The tangents drawn at the extremities of the diameter of a circle are ______.
Find the value of ∠DCE.

Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

