Advertisements
Advertisements
प्रश्न
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
उत्तर
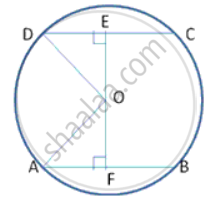
AF = FB = 8.4 cm
And DE = EC ----(1)
(Perpendicular from centre to a chord bisects the chord)
In right Δ ODA,
By Pythagoras theorem, OA2 = OF2 + AF2
= (11.2)2 + (8.4)2
= 125.44 + 70.56
OA2 = 196
OA = 14 cm
OA = OD = 14cm (radii of same circle)
Similarly, In Δ DEO
OD2 = OE2 + DE2
DE2 = 142 + 8.42
= 196 - 70.56
DE2 = 125.44
DE = 11.2 cm
∴ length of chord DC = 2DE = 2(11.2) = 22.4 cm
APPEARS IN
संबंधित प्रश्न
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

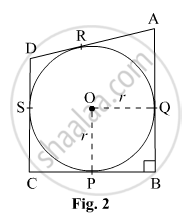
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
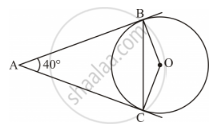
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
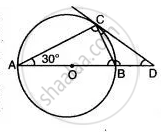
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

The distance between two parallel tangents of a circle of radius 4 cm is ______
Tangents from an external point to a circle are ______
The quadrilateral formed by joining the angle bisectors of a cyclic quadrilateral is a ______
How many tangents can be drawn to a circle from a point on it?
