Advertisements
Advertisements
प्रश्न
A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
उत्तर
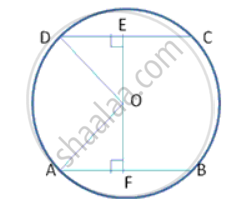
AF = FB = 3cm
CE = ED = 7.2cm
(Perpendicular from centre to a chord bisects the chord)
In right Δ AFO, By Pythagoras theorem,
OA2 =OF2+ AF2
OA2 = (7.2)2 + (3)2
OA2 = 51.84 + 9
OA2 = 60.84
OA = 7.8cm
OA = OC = 7.8cm (radii of same circle)
Similarly, In right Δ OFC,
OC2 = OE2 + EC2
OE2 = (7 .8)2 - (7.2)2
= 60.84 - 51.84
OE2 = 9
OE = 3cm
Distance from centre of chord CD with length 14.4cm is 3cm.
APPEARS IN
संबंधित प्रश्न
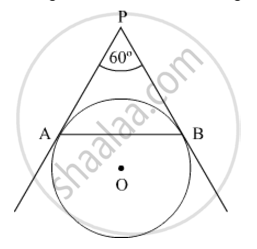
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
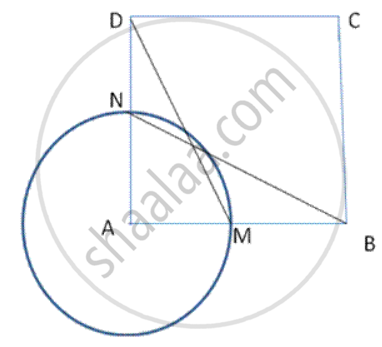
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
The area of the shaded portion in the following figure is equal to the area of.
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.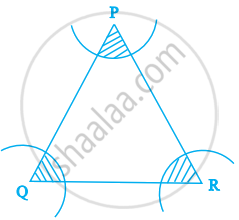
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
