Advertisements
Advertisements
प्रश्न
A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
उत्तर
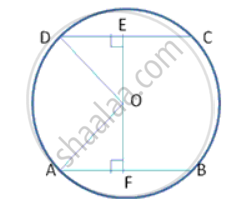
AF = FB = 3cm
CE = ED = 7.2cm
(Perpendicular from centre to a chord bisects the chord)
In right Δ AFO, By Pythagoras theorem,
OA2 =OF2+ AF2
OA2 = (7.2)2 + (3)2
OA2 = 51.84 + 9
OA2 = 60.84
OA = 7.8cm
OA = OC = 7.8cm (radii of same circle)
Similarly, In right Δ OFC,
OC2 = OE2 + EC2
OE2 = (7 .8)2 - (7.2)2
= 60.84 - 51.84
OE2 = 9
OE = 3cm
Distance from centre of chord CD with length 14.4cm is 3cm.
APPEARS IN
संबंधित प्रश्न
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
A car has two wipers which do not overlap. Each wiper has blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades [Use π = `22/7`]
A round table cover has six equal designs, as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs.0.35 per cm2. [Use `sqrt3 = 1.7`]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
