Advertisements
Advertisements
рдкреНрд░рд╢реНрди
The area of sector of circle of radius 2cm is ЁЭЬЛcm2. Find the angle contained by the sector.
рдЙрддреНрддрд░
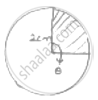
Area of sector = ЁЭЬЛ ЁЭСРЁЭСЪ2
Radius of circle = 2ЁЭСРЁЭСЪ
Let ЁЭЬГ = angle subtended by arc at centre
Area of sector =`theta/360^@× pir^2`
=`theta/360^@× pi× 2 × 2`
=`(pitheta)/90^@`
`(pitheta)/90^@`= ЁЭЬЛ ⇒ ЁЭЬГ = 90°
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
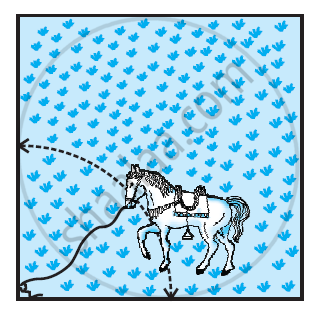
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
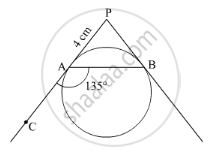
In the given figure, PA and PB are tangents to a circle from an external point P such that PA = 4 cm and ∠BAC = 135°. Find the length of chord AB ?
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
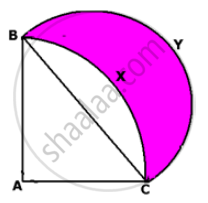
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
In figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and distance between AB and DC = 14 cm. If arcs of equal radii 7 cm with centres A, B, C and D have been drawn, then find the area of the shaded region of the figure.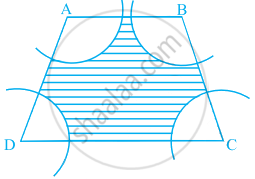
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
