Advertisements
Advertisements
प्रश्न
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
उत्तर
We know that the area of minor segment of angle `theta` in a circle of radius r is,
`A={(pitheta)/360^@-"sin"theta/2 "cos"theta/2}r^2`
It is given that the chord AB divides the circle in two segment.
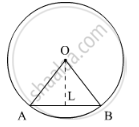
We have OA=4 cm and AB=4 cm. so,
`AL=(AB)/2 cm`
`=4/2 cm`
= 2 cm
Let `angleAOB=2theta`. Then,
`angleAOL=angleBOL`
`=theta`
In`triangleOLA`,We have
`sintheta=(AL)/(OA)`
`=2/4`
`=1/2`
`theta="sin"^(-1)1/2`
`=30^@`
Hence, `angleAOB=60^@`
Now using the value of r and `theta`, we will find the area of minor segment
`A={(pixx60^@)/360^@-"sin"60^@/2"cos"60^@/2}xx4xx4`
`={pi/6-sin30^@cos30^@}xx16`
`={(16xxpi)/6-1/2xxsqrt(3)/2xx16}`
`={(8pi)/3-4sqrt(3)}cm^2`
APPEARS IN
संबंधित प्रश्न
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
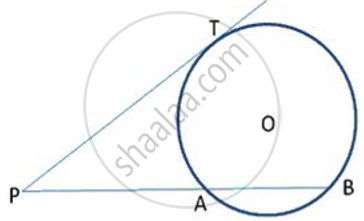
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.
A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
