Advertisements
Advertisements
प्रश्न
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
विकल्प
2800
4000
5500
7000
उत्तर
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is 7000.
Explanation:

Here,
Number of revolutions = `"Total distance"/("Distance covered in" 1 "revolution")`
Given,
Radius = 0.25 m
Total Distance = 11 km = 11,000 m
Therefore,
Distance covered in one revolution = Circumference of wheel
= 2πr
= `2 xx 22/7 xx 0.25`
= `2 xx 22/7 xx 1/4`
= `11/7` m
Now,
Number of revolutions = `"Total distance"/("Distance covered in" 1 "revolution")`
= `11000/(11/7)`
= `11000 xx 7/11`
= 1000 × 7
= 7000
APPEARS IN
संबंधित प्रश्न
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
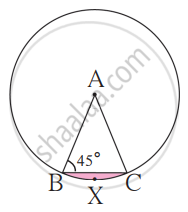
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m × 16 m. Find the area of the field in which the cow can graze.
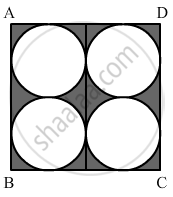
In the given figure, find the area of the shaded region, where ABCD is a square of side 14 cm and all circles are of the same diameter.
The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
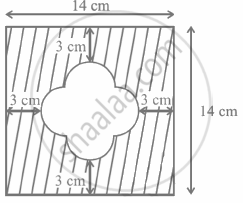
Find the area of the unshaded region shown in the given figure.