Advertisements
Advertisements
प्रश्न
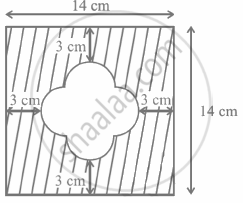
Find the area of the unshaded region shown in the given figure.
उत्तर
The side of a square = Diameter of the semi-circle = a
Area of the unshaded region
= Area of a square of side ‘a’ + 4(Area of a semi-circle of diameter ‘a’)
The horizontal/vertical extent of the white region = 14 – 3 – 3 = 8 cm
Radius of the semi-circle + Side of a square + Radius of the semi-circle = 8 cm
2 (radius of the semi-circle) + Side of a square = 8 cm
2a = 8 cm
`\implies` a = 4 cm
Area of the unshaded region
= Area of a square of side 4 cm + 4 (Area of a semi-circle of diameter 4 cm)
= `(4)^2 + 4 xx 1/2 π(2)^2`
= (16 + 8π) cm2
APPEARS IN
संबंधित प्रश्न
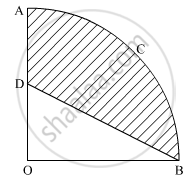
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
Find the perimeter of a quadrant of a circle of radius 14 cm.
