Advertisements
Advertisements
प्रश्न
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
उत्तर
Given that, three circles are in such a way that each of them touches the other two.
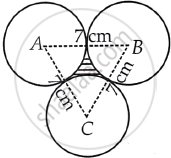
Now, join AB, BC and CA.
Since, radius of each circle is 3.5 cm.
So, AB = 2 × radius of circle
= 2 × 3.5 cm
= 7 cm
∴ AC = BC = AB = 7 cm
So, ΔABC is an equilateral triangle with side 7 cm.
We know that, each angle between two adjacent sides of an equilateral triangle is 60°.
∴ Area of sector with ∠A = 60°
= `(∠"A")/360^circ xx pi"r"^2`
= `60^circ/360^circ xx pi xx (3.5)^2 "cm"^2`
So, area of each sector = 3 × area of sector with angle A
= `3 xx 60^circ/360^circ xx pi xx (3.5)^2 "cm"^2`
= `1/2 xx 22/7 xx 3.5 xx 3.5 "cm"^2`
= `11 xx 5/10 xx 35/10 "cm"^2`
= `77/4 "cm"^2`
= 19.25 cm2
And area of ΔABC = `sqrt(3)/4 xx (7)^2 "cm"^2` ...[∵ Area of an equilateral triangle = `sqrt(3)/4 xx ("side")^2`]
= `(49sqrt(3))/4 "cm"^2`
∴ Area of shaded region enclosed between these circles
= Area of ΔABC – Area of each sector
= `(49sqrt(3))/4 - 19.25`
= `12.25 xx sqrt(3) - 19.25`
= 21.2176 – 19.25
= 1.9676 cm2
Hence, the required area enclosed between these circles is 1.967 cm2 (approx).
APPEARS IN
संबंधित प्रश्न
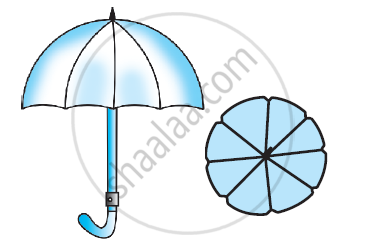
An umbrella has 8 ribs which are equally spaced. Assuming umbrella to be a flat circle of radius 45 cm. Find the area between the two consecutive ribs of the umbrella.
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
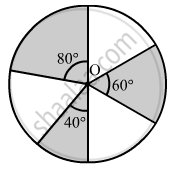
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
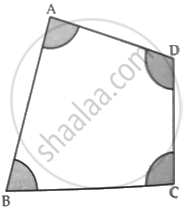
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
The area of the sector of a circle of radius 12 cm is 60π cm2. The central angle of this sector is ______.
