Advertisements
Advertisements
प्रश्न
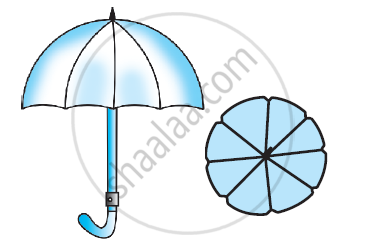
An umbrella has 8 ribs which are equally spaced. Assuming umbrella to be a flat circle of radius 45 cm. Find the area between the two consecutive ribs of the umbrella.
उत्तर
Since ribs are equally spaced. Therefore, Angle made by two consecutive ribs at the centre = `\frac { 360° }{ 8 } = 45º`
Area of sector = `theta/(360º) xx pir^2`
`= (45º)/(360º) xx 22 /7 xx 45xx45`
`= (11 xx 45xx 45)/(4xx7)`cm2
`= 22275/28` cm2
The required area between the two consecutive ribs `= 22275/28` cm2
APPEARS IN
संबंधित प्रश्न
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
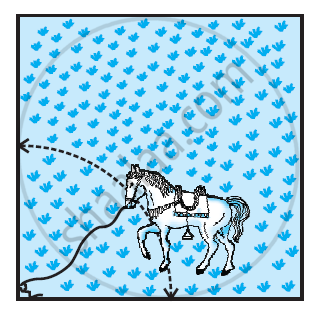
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). Find
- The area of that part of the field in which the horse can graze.
- The increase in the grazing area of the rope were 10 m long instead of 5 m. [Use π = 3.14]
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
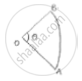
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. ( \[\pi\] = 3.14 ).
In the given figure, if O is the center of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of the shaded region is 114 cm2, find the radius of the circle. \[\pi\] = 3.14)

A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
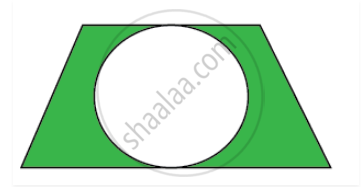
In the given figure, a circle is inscribed in a trapezium of height 14 cm and lengths of parallel sides are equal to 25 cm and 40 cm. What is the area of the shaded region?
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
Find the perimeter of a quadrant of a circle of radius 14 cm.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
