Advertisements
Advertisements
प्रश्न
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
उत्तर
According to the question,
The four circles are placed such that each piece touches the other two pieces.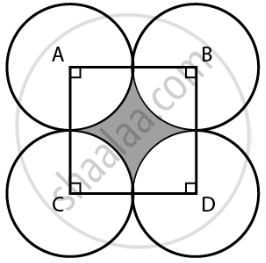
By joining the centres of the circles by a line segment, we get a square ABDC with sides,
AB = BD = DC = CA = 2 ...(Radius)
= 2(7) cm
= 14 cm
Now, Area of the square = (Side)2
= (14)2
= 196 cm2
ABDC is a square,
Therefore, each angle has a measure of 90°.
i.e., ∠A = ∠B = ∠D = ∠C = 90° = `pi/2` radius = θ ...(say)
Given that,
Radius of each sector = 7 cm
Area of the sector with central angle A = `(1/2)"r"^2θ`
= `1/2"r"^2θ`
= `1/2 xx 49 xx pi/2`
= `1/2 xx 49 xx 22/(2 xx 7)`
= `77/2 "cm"^2`
Since the central angles and the radius of each sector are same, area of each sector is `77/2 "cm"^2`
∴ Area of the shaded portion = Area of square – Area of the four sectors
= `196 - (4 xx 77/2)`
= 196 – 154
= 42 cm2
Therefore, the required area of the portion enclosed between these pieces is 42 cm2.
APPEARS IN
संबंधित प्रश्न
A car has two wipers which do not overlap. Each wiper has blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades [Use π = `22/7`]
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the minor segment. [Use π = 3.14.]
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
If the area of a circle is numerically equal to twice its circumference, then the diameter of the circle is ____________.
If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
