Advertisements
Advertisements
प्रश्न
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
उत्तर
According to the question,
The four circles are placed such that each piece touches the other two pieces.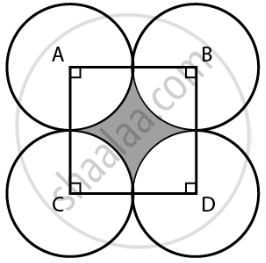
By joining the centres of the circles by a line segment, we get a square ABDC with sides,
AB = BD = DC = CA = 2 ...(Radius)
= 2(7) cm
= 14 cm
Now, Area of the square = (Side)2
= (14)2
= 196 cm2
ABDC is a square,
Therefore, each angle has a measure of 90°.
i.e., ∠A = ∠B = ∠D = ∠C = 90° = `pi/2` radius = θ ...(say)
Given that,
Radius of each sector = 7 cm
Area of the sector with central angle A = `(1/2)"r"^2θ`
= `1/2"r"^2θ`
= `1/2 xx 49 xx pi/2`
= `1/2 xx 49 xx 22/(2 xx 7)`
= `77/2 "cm"^2`
Since the central angles and the radius of each sector are same, area of each sector is `77/2 "cm"^2`
∴ Area of the shaded portion = Area of square – Area of the four sectors
= `196 - (4 xx 77/2)`
= 196 – 154
= 42 cm2
Therefore, the required area of the portion enclosed between these pieces is 42 cm2.
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
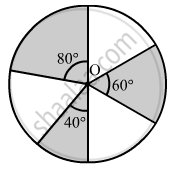
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

Four cows are tethered at the four corners of a square field of side 50 m such that each can graze the maximum unshared area. What area will be left ungrazed?
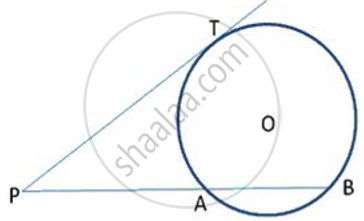
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
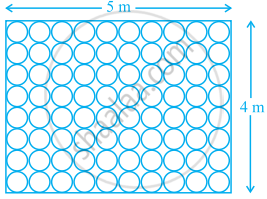
Floor of a room is of dimensions 5 m × 4 m and it is covered with circular tiles of diameters 50 cm each as shown in figure. Find the area of floor that remains uncovered with tiles. (Use π = 3.14)
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
