Advertisements
Advertisements
प्रश्न
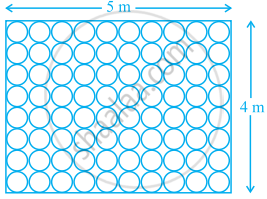
Floor of a room is of dimensions 5 m × 4 m and it is covered with circular tiles of diameters 50 cm each as shown in figure. Find the area of floor that remains uncovered with tiles. (Use π = 3.14)
उत्तर
Given, floor of a room is covered with circular tiles.
Length of a floor of a room (l) = 5 m
And breadth of floor of a room (b) = 4 m
∴ Area of floor of a room = l × b
= 5 × 4
= 20 m2
⇒ Radius of each circular tile (r) = `50/2 "cm"`
= 25 m
= `25/100 "m"`
= `1/4 "m"`
Now, area of a circular tile = πr2
= `3.14 xx (1/4)^2 "m"^2`
= `3.14/16 "m"^2`
∴ Number of circular tiles = 80
∴ Area of 80 circular tiles
= `80 xx 3.14/16`
= 5 × 3.14
= 15.7 m2
So, area of floor that remains uncovered with tiles = Area of floor of a room – Area of 80 circular tiles
= 20 – 15.7
= 4.3 m2
Hence, the required area of floor that remains uncovered with tiles is 4.3 m2.
APPEARS IN
संबंधित प्रश्न
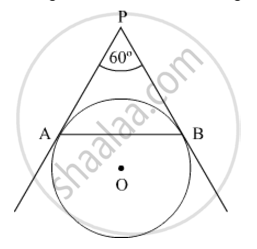
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. ( \[\pi\] = 3.14 ).
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

The area of the shaded portion in the following figure is equal to the area of.
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
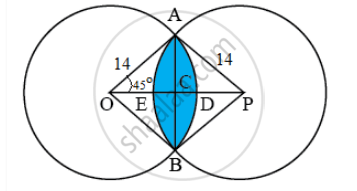
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
