Advertisements
Advertisements
प्रश्न
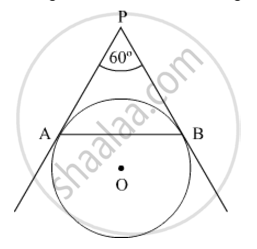
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
उत्तर
PA and PB are tangents drawn to the given circle from an external point P.
It is known that the lengths of the tangents drawn from an external point to a circle are equal.
∴ PA = PB
In ∆PAB, sides PA and PB are of the same length.
Hence, ∆PAB is isosceles, with PA = PB and ∠PAB = ∠PBA = x (say).
It is given that
∠APB = 60°
We know that the sum of the angles of a triangle is 180°
In ∆PAB,
∠PAB + ∠PBA + ∠APB = 180°
∴ x + x + 60° = 180°
⇒ 2x = 120°
⇒ x = 60°
Thus,
∠PAB = ∠PBA = ∠APB = 60°
Since all angles of ∆PAB are of the same measure, ∆PAB is equilateral, with AP = BP = AB.
It is given that
AP = 5 cm
∴ AB = AP = 5 cm
Thus, the length of the chord AB is 5 cm.
APPEARS IN
संबंधित प्रश्न
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
(2) Area of any one of the sectors
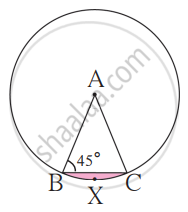
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
Three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these circles.
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
What is the length of arc of a circle of radius 7 cm which subtends an angle of 90° at the centre of the circle?
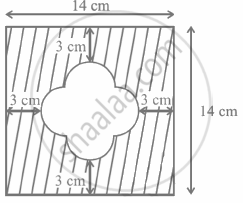
Find the area of the unshaded region shown in the given figure.