Advertisements
Advertisements
प्रश्न
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
पर्याय
2800
4000
5500
7000
उत्तर
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is 7000.
Explanation:

Here,
Number of revolutions = `"Total distance"/("Distance covered in" 1 "revolution")`
Given,
Radius = 0.25 m
Total Distance = 11 km = 11,000 m
Therefore,
Distance covered in one revolution = Circumference of wheel
= 2πr
= `2 xx 22/7 xx 0.25`
= `2 xx 22/7 xx 1/4`
= `11/7` m
Now,
Number of revolutions = `"Total distance"/("Distance covered in" 1 "revolution")`
= `11000/(11/7)`
= `11000 xx 7/11`
= 1000 × 7
= 7000
APPEARS IN
संबंधित प्रश्न
In the following figure, if m(are DXE) = 90° and m(are AYC) = 30°. Find ∠DBE.

Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60˚. Also find the area of the corresponding major segment.[use π=22/7]
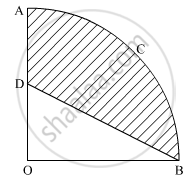
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector
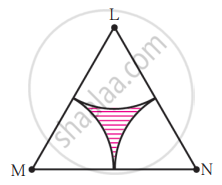
(2) Area of any one of the sectors
In the given figure, O is the centre of the circle. m ( arc PQR) = 60° OP = 10 cm. Find the area of the shaded region.( \[\pi\]= 3.14, \[\sqrt{3}\]= 1.73)

The length of the minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6 : 05 am and 6 : 40 am.
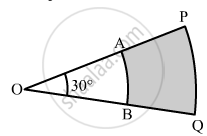
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
