Advertisements
Advertisements
प्रश्न
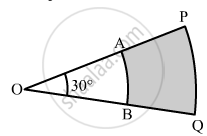
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
उत्तर
Area of the shaded portion = Area of sector OPQ − Area of sector OAB
`= 30^circ/360xxpi(7)^2 - 30^circ/360^circxxpi(3.5)^2`
`=22/7xx1/12[(7)^3 - (3.5)^2]`
`= 22/7 xx 1/12[(7)^2-(7/2)^2]`
`=22/7xx1/12xx147/4`
`=77/8 "cm"^2`
Hence, the area of the shaded portion is`77/8` cm2 .
APPEARS IN
संबंधित प्रश्न
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
Choose the correct alternative answer for the following question.
Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
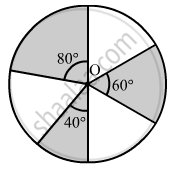
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
The areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal? Why?
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
The length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle is ______.
