Advertisements
Advertisements
प्रश्न
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
उत्तर
Let the diagonal of the square be d.
We know that if a circle circumscribes a square, then the diameter of the circle is equal to the diagonal of the square.
∴ d = 2 × 7 = 14 cm
Now,
Area of required region = Area of circle - Area of square
`=pi"r"^2 - 1/2d^2`
`= 22/7 xx(7)^2 - 1/2xx(14)^2`
= 56 cm2
Hence, the required area is 56 cm2 .
APPEARS IN
संबंधित प्रश्न
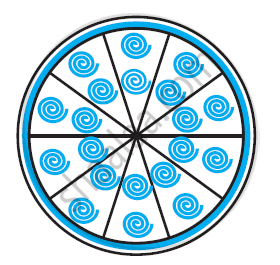
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. Find.
- The total length of the silver wire required.
- The area of each sector of the brooch [Use π = `22/7`]
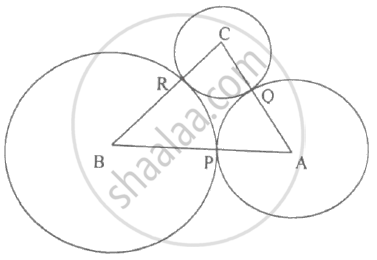
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
The diagram shows a sector of circle of radius ‘r’ can containing an angle 𝜃. The area of sector is A cm2 and perimeter of sector is 50 cm. Prove that
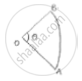
(i) 𝜃 =`360/pi(25/r− 1)`
(ii) A = 25r – r2
A chord AB of circle, of radius 14cm makes an angle of 60° at the centre. Find the area of minor segment of circle.
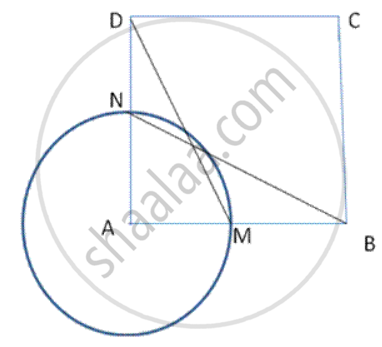
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is ______.
The circumference of a circle is 100 cm. The side of a square inscribed in the circle is ______.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
