Advertisements
Advertisements
प्रश्न
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
उत्तर
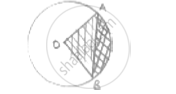
AB is chord AB = 4cm
OA = OB = 4cm
OAB is equilateral triangle ∠AOB = 60°
Area of sector (formed by chord [shaded region]) = (area of sector)
`=theta/360^@× pir^2 =60/360× pi × 4 × 4 =(8pi)/3 cm^2`
APPEARS IN
संबंधित प्रश्न
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
Major sector [Use π = 3.14]
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. [Use π = 3.14 and `sqrt3 = 1.73`]
A sector is cut-off from a circle of radius 21 cm the angle of sector is 120°. Find the length of its arc and its area.
A sector of 56° cut out from a circle contains area of 4.4 cm2. Find the radius of the circle
A chord of length 6 cm is at a distance of 7.2 cm from the centre of a circle. Another chord of the same circle is of length 14.4 cm. Find its distance from the centre.
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
Find the area of the sector of a circle of radius 8 cm and arc with length 15 cm.
Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
Find the perimeter of a quadrant of a circle of radius 14 cm.
The length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle is ______.
