Advertisements
Advertisements
प्रश्न
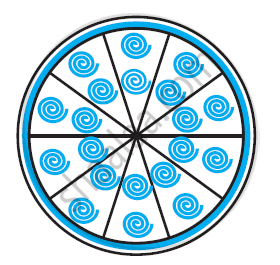
A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. Find.
- The total length of the silver wire required.
- The area of each sector of the brooch [Use π = `22/7`]
उत्तर
Total length of wire required will be the length of 5 diameters and the circumference of the brooch.
Radius of circle = `35/2` mm
Circumference of brooch = 2πr
`= 2 xx 22/7xx (35/2)`
= 110 mm
Length of wire required = 110 + 5 × 35
= 110 + 175 = 285 mm
It can be observed from the figure that each of 10 sectors of the circle is subtending 36° at the centre of the circle
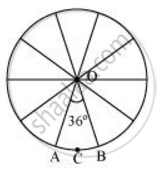
Therefore, area of each sector = `36^@/360^@ xx pir^2`
`=1/10xx22/7xx(35/2)xx(35/2)`
= `385/4` mm2
APPEARS IN
संबंधित प्रश्न
Find the area of sector whose arc length and radius are 10 cm and 5 cm respectively
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. [Use π = 3.14 and `sqrt3 = 1.73` ]
Area of a sector of angle p (in degrees) of a circle with radius R is ______.
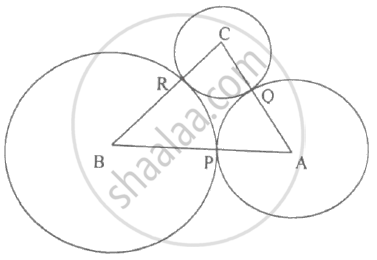
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`

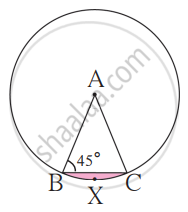
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
Find the difference of the areas of two segments of a circle formed by a chord of length 5 cm subtending an angle of 90° at the centre.
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
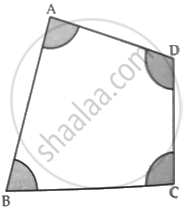
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
