Advertisements
Advertisements
प्रश्न
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
उत्तर
Given: The radius of a circle (r) = 10 cm
Measure of an arc of the circle (θ) = 54°
Area of the sector = `θ/360^circ` × πr2
= `bb54/360^circ` × 3.14 × 10 × 10
= 3 × 1.57 × 10
= 47.10 cm2
APPEARS IN
संबंधित प्रश्न
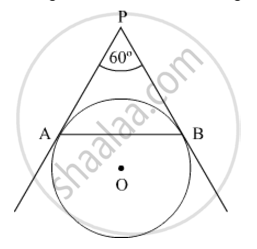
In Fig. 3, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships warned. [Use π = 3.14]
A sector of circle of radius 4cm contains an angle of 30°. Find the area of sector
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.
AB is a chord of circle with centre O and radius 4cm. AB is length of 4cm. Find the area of sector of the circle formed by chord AB
The perimeter of a sector of circle of radius 5.7m is 27.2 m. Find the area of sector.
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
A chord of circle of radius 14cm makes a right angle at the centre. Find the areas of minor and major segments of the circle.
A chord 10 cm long is drawn in a circle whose radius is 5√2 cm. Find the area of both
segments
The radius of a circle is 10 cm. The area of a sector of the sector is 100 cm2. Find the area of its corresponding major sector. ( \[\pi\] = 3.14 ).

(2) Area of any one of the sectors
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

In following figure , C is a point on the minor arc AB of the circle with centre O . Given ∠ ACB = p° , ∠ AOB = q° , express q in terms of p. Calculate p if OACB is a parallelogram.

In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

Find the area of the shaded region where ABC is a quadrant of radius 5cm and a semicircle is drawn with BC as diameter.
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
In figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
