Advertisements
Advertisements
Question
In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
Solution
Let the diagonal of the square be d.
We know that if a circle circumscribes a square, then the diameter of the circle is equal to the diagonal of the square.
∴ d = 2 × 7 = 14 cm
Now,
Area of required region = Area of circle - Area of square
`=pi"r"^2 - 1/2d^2`
`= 22/7 xx(7)^2 - 1/2xx(14)^2`
= 56 cm2
Hence, the required area is 56 cm2 .
APPEARS IN
RELATED QUESTIONS
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60° [Use `pi = 22/7`]
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
In fig. 6, AB is a chord of a circle, with centre O, such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P. Find the length of PA ?

In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

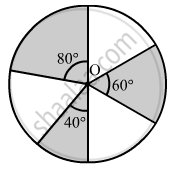
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
Four cows are tethered at the four corners of a square field of side 50 m such that the each can graze the maximum unshared area. What area will be left ungrazed?
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point of intersection of its diagonals.
Find the area of a sector of a circle having radius 6 cm and length of the arc 15 cm.
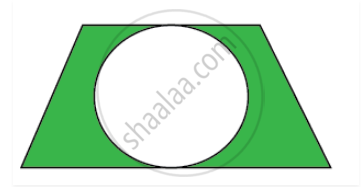
In the given figure, a circle is inscribed in a trapezium of height 14 cm and lengths of parallel sides are equal to 25 cm and 40 cm. What is the area of the shaded region?