Advertisements
Advertisements
Question
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
Solution
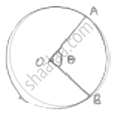
𝜃 = angle subtended at centre
Radius (r) = 5.6m = OA ± OB
Perimeter of sector = 27.2 m
(AB arc length) + OA + OB = 27.2
⇒`(theta/360^@× 2pir)` + 5.6 + 5.6 ± 27.2
⇒`(5.6 pitheta)/180^@`+ 11.2 = 27.2
⇒ `5.6 ×22/7`× 𝜃 = 16 × 180
⇒ 𝜃 `=(16×180)/(0.8×22)`= 163.64°
Area of sector =`theta/360^@× pir^2 =163.64^@/360^@×22/7`× 5.6 × 5.6
=`163.64/180`× 11 × 0.8 × 5.6
= 44.8 cm2
APPEARS IN
RELATED QUESTIONS
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
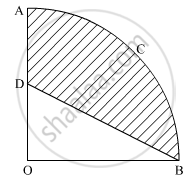
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
The area of sector of circle of radius 2cm is 𝜋cm2. Find the angle contained by the sector.

In the given figure, if A is the centre of the circle. \[\angle\] PAR = 30°, AP = 7.5, find the area of the segment PQR. (\[\pi\] = 3.14)

In the given figure, if O is the center of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of the shaded region is 114 cm2, find the radius of the circle. \[\pi\] = 3.14)

In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

A chord 10 cm long is drawn in a circle whose radius is `5sqrt(2)` cm. Find the areas of both the segments.
A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 7 m long rope. The area of that part of the field in which the horse can graze is ____________.
The length of the minute hand of a clock is 6 cm. Find the area swept by it when it moves from 7:05 p.m. to 7:40 p.m.
