Advertisements
Advertisements
Question
A sector is cut-off from a circle of radius 21 cm the angle of sector is 120°. Find the length of its arc and its area.
Solution

Radius of circle (r) = 21 cm
𝜃 = angle subtended at centre = 120°
Length of its arc =`theta/360^@`× 2𝜋𝑟
=`120/360× 2 ×22/7× 21`
= 44 cms
Area of sector =`theta/360^@× pir^2`
=`120/360×22/7`× 21 × 21
= (22 × 21)
= 462 cm2
𝐿𝑒𝑛𝑔𝑡ℎ 𝑜𝑓 𝑎𝑟𝑐 = 44 𝑐𝑚
Area of sector = 462 cm2
APPEARS IN
RELATED QUESTIONS
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [Use `pi = 22/7`]
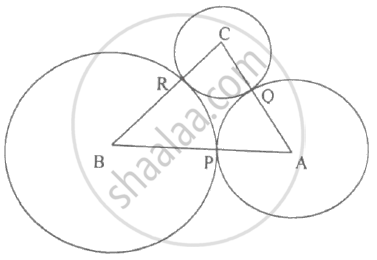
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.
The perimeter of certain sector of circle of radius 5.6 m is 27.2 m. Find the area of sector.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`
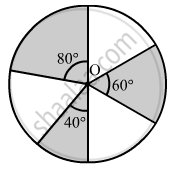
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
The area of the sector of a circle of radius 10.5 cm is 69.3 cm2. Find the central angle of the sector.
In figure, arcs are drawn by taking vertices A, B and C of an equilateral triangle of side 10 cm. to intersect the sides BC, CA and AB at their respective mid-points D, E and F. Find the area of the shaded region (Use π = 3.14).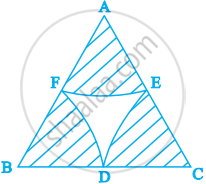
Four circular cardboard pieces of radii 7 cm are placed on a paper in such a way that each piece touches other two pieces. Find the area of the portion enclosed between these pieces.
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
