Advertisements
Advertisements
Question
Find the area of the sector of a circle of radius 7 cm and of central angle 90°. Also, find the area of corresponding major sector.
Solution
Given that,
Radius of circle = 7 cm
Central angle = 90°
Now, area of minor sector of circle
= `(πr^2θ)/360^circ`
= `(π(7)^2)/4`
= `(22 xx 7 xx 7)/(7 xx 4)`
= 38.5 cm2
Area of complete circle
= πr2
= π(7)2
= 154 cm2
Now, area of major sector
= Area of complete circle – Area of minor sector
= 154 – 38.5
= 115.5 cm2
APPEARS IN
RELATED QUESTIONS
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of arc and area of sector
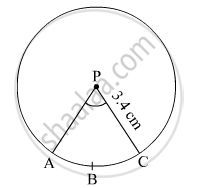
In the given figure, radius of circle is 3.4 cm and perimeter of sector P-ABC is 12.8 cm . Find A(P-ABC).
In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

A chord PQ of a circle with a radius of cm subtends an angle of 60° with the center of the circle. Find the area of the minor as well as the major segment. ( \[\pi\] = 3.14, \[\sqrt{3}\] = 1.73)
In the given figure, ABCD is a square of side 7 cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.

In a circle of radius 7 cm, a square ABCD is inscribed. Find the area of the circle which is outside the square.
In the following figure, if m(arc DXE) = 120° and m(arc AYC) = 60°. Find ∠DBE.

The area of the shaded portion in the following figure is equal to the area of.
In the given figure, a circle is inscribed in a trapezium of height 14 cm and lengths of parallel sides are equal to 25 cm and 40 cm. What is the area of the shaded region?
The area of the sector of a circle of radius 12 cm is 60π cm2. The central angle of this sector is ______.
